
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Коды Хемминга. Матричная запись кода. Покажите на примере кода (7,4)
1. Код, содержащий  кодовых слов в разрешенном наборе, может быть задан k линейно-независимыми векторами
кодовых слов в разрешенном наборе, может быть задан k линейно-независимыми векторами  составляющими базисную матрицу L размером
составляющими базисную матрицу L размером 
 ` (9.17)
` (9.17)
Множество разрешенных кодовых слов, определяемое базисной матрицей L, обозначим BL. Любое кодовое слово из разрешенного набора BL, определяемого матрицей (9.17), может быть представлено в виде линейной композиции входящих в нее векторов:

 . (9.18)
. (9.18)
Нетрудно видеть, что общее число разрешенных кодовых слов, образуемых по закону (9.18), равно числу различных комбинаций из k коэффициентов  принимающих одно из значений 0,1, ... m - 1 т.е. закон (9.18) обеспечивает образование заданного числа M = mk различных кодовых слов длиной п. Таким образом, базисная матрица размером
принимающих одно из значений 0,1, ... m - 1 т.е. закон (9.18) обеспечивает образование заданного числа M = mk различных кодовых слов длиной п. Таким образом, базисная матрица размером  задает линейный код (n, k).
задает линейный код (n, k).
Простой код является линейным кодом (n, n), базисная матрица которого включает полный набор n-мерных линейно-независимых векторов (число линейно-независимых векторов в n-мерном пространстве не может превосходить п).
2. Множеству разрешенных кодовых слов  , определяемому матрицей L, отвечает некоторое множество
, определяемому матрицей L, отвечает некоторое множество  кодовых слов, ортогональных кодовым словам разрешенного набора: если
кодовых слов, ортогональных кодовым словам разрешенного набора: если  , а
, а 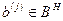 , то
, то  . Множество
. Множество  может быть задано п - k линейно-независимыми векторами, составляющими матрицу Н размером
может быть задано п - k линейно-независимыми векторами, составляющими матрицу Н размером  :
:

Матрица H называется проверочной. Множество  содержит
содержит  кодовых слов, отвечающих всем возможным линейным композициям векторов, составляющих матрицу H. Свойства множеств
кодовых слов, отвечающих всем возможным линейным композициям векторов, составляющих матрицу H. Свойства множеств  и
и  взаимны: множество
взаимны: множество  также представляет линейный код, для которого матрица H является базисной, а матрица L — проверочной.
также представляет линейный код, для которого матрица H является базисной, а матрица L — проверочной.
Проверочная матрица H так же, как и базисная матрица L, полностью определяет линейный код. Она позволяет представить линейный код (n, k) в систематической форме:
 (9.19)
(9.19)
где первые k символов  — информационные, а последние n-k символов
— информационные, а последние n-k символов  — избыточные, обеспечивающие возможность обнаружения и исправления ошибок (их называют проверочными символами).
— избыточные, обеспечивающие возможность обнаружения и исправления ошибок (их называют проверочными символами).
Проверочные символы разрешенного кодового слова  при заданных информационных символах
при заданных информационных символах  могут быть определены из n-k линейных уравнений, определяемых условиями ортогональности разрешенного кодового слова кодовым словам проверочной матрицы H:
могут быть определены из n-k линейных уравнений, определяемых условиями ортогональности разрешенного кодового слова кодовым словам проверочной матрицы H:

 . (9.20)
. (9.20)
Уравнения (9.20) можно переписать в виде:
 ,
,  (9.21)
(9.21)
Разрешая систему n-k уравнений (9.21) относительно n-k проверочных символов  , получим для них линейные выражения вида
, получим для них линейные выражения вида
 ,
,  . (9.22)
. (9.22)
Формула (9.22) позволяет определить n-k проверочных символов  , разрешенного кодового слова по известным k информационным символам (коэффициенты
, разрешенного кодового слова по известным k информационным символам (коэффициенты  , определяющие закон формирования проверочных символов, выражаются через элементы
, определяющие закон формирования проверочных символов, выражаются через элементы  проверочной матрицы H).
проверочной матрицы H).
Формула (9.22) является весьма удобной формой задания регулярного линейного кода (n, k), широко используемой в практике связи. При этом для образования разрешенных кодовых слов по известным информационным символам достаточно хранить в памяти  значений коэффициентов
значений коэффициентов  , водящих в (9.22). Поскольку при задании кода с основанием m для каждого из этих коэффициентов может быть выбрано одно из т значений, то всегда можно выбрать
, водящих в (9.22). Поскольку при задании кода с основанием m для каждого из этих коэффициентов может быть выбрано одно из т значений, то всегда можно выбрать  вариантов коэффициентов в (9.22) и построить
вариантов коэффициентов в (9.22) и построить  различных линейный кодов (n, k). Задача заключается в том, чтобы выбрать оптимальный вариант кода
различных линейный кодов (n, k). Задача заключается в том, чтобы выбрать оптимальный вариант кода
Дата добавления: 2015-04-21; просмотров: 219; Мы поможем в написании вашей работы!; Нарушение авторских прав |