
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Замыкание множества функциональных зависимостей
Пусть R – универсальная схема отношения;
F – заданное множество функциональных зависимостей на этой схеме.
Замыканием F назовем множество функциональных зависимостей, которые логически следуют из F.
Функциональная зависимость логически следует из F, если её можно получить с помощью аксиом Армстронга. Обозначается F+ .
Аксиомы Армстронга (правила вывода)
1) Аксиомы рефлексивности
Если 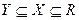 , то X →Y
, то X →Y
2) Аксиома пополнения
Пусть X →Y, 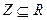 (Z может быть Ø)
(Z может быть Ø)
Тогда 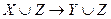 (XZ →YZ)
(XZ →YZ)
3) Аксиома транзитивности
Если X →Y, Y→Z, то X →Z
Лекция 8
Пример построения замыкания.
(А,В,С)
F=(АàB, BàС)
F+-?
1) Построение тривиальных функциональных зависимостей:
AàA, BàB, CàC, ABàA, ABàB, ACàA, ACàC, BCàC, BCàB, ABCàA, ABCàC, ABCàB, ABCàAC, ABCàAB, ABCàBC, ABCàABC, ABàAB, ACàAC, BCàBC
2) Используем вторую аксиому Армстронга
AàAB
АСàBC
BàBC
ABàAC
ACàABC
ABàABC
3) Используем третью аксиому Армстронга
Т.к. АàB, BàС, то AàC
Аналогично, ABàBC, AàAC, AàABC
Лемма
Справедливы следующие правила:
1) Правило объединения
Если множество атрибутов Х определяет множество атрибутов У (XàY) и XàZ, то XàYZ
2) Правило декомпозиции:
Если XàY, ZÍY, то XàZ
3) Правило псевдотранзитивности:
Если XàY, WYàZ,то WXàZ
Доказательство:
1. XàХY (пополняем атрибутом Х первую зависимость)
XYàYZ (пополняем атрибутом Y вторую зависимость)
По третьей аксиоме Армстронга получаем XàYZ
2. Т.к. XàY, ZÍY, то по первой аксиоме Армстронга YàZ. Тогда по 3 аксиоме получаем: XàZ
3. WXàWY (пополняем атрибутом W первую зависимость)
WYàZ (по условию). Тогда по 3 аксиоме получаем: WXàZ
Теорема
Аксиомы Армстронга являются надежными и полными.
Надежность: если функциональная зависимость выводится с помощью аксиомы Армстронга, то она справедлива в любых экземплярах отношений, где справедливы исходные функциональные зависимости.
Полнота: если имеет место функциональная зависимость XàY, то она обязательно может быть выведена с помощью аксиом Армстронга.
Количество функциональных зависимостей, входящих в замыкание F+, может быть очень велико, даже если число исходных функциональных зависимостей незначительно.
Пример
F={XàA1…. XàAn}
Из правила объединения следует, что справедлива функциональная зависимость XàY, где Y- произвольное подмножество множества (A1…. An). Таких комбинаций может быть 2n.
Поэтому в теории нормализации схем отношений напрямую замыкание F+ не строится, но есть подход, позволяющий определить, принадлежит ли функциональная зависимость XàY замыканию F+. Этот подход основывается на понятии замыкания множества атрибутов.
Замыкание множества атрибутов.
Пусть R- универсальная схема отношений. Замыканием множества атрибутов Х, принадлежащего R (XÍR), называется множество атрибутов Ai1…. Aik, таких, что справедливо следующее выражение:
(XàAi1…. XàAik) ÍF+.
Замыкание множества атрибутов обозначается через Х+.
Правило
Чтобы проверить, принадлежит ли функциональная зависимость XàY замыканию F+ (XàY ÍF+), сначала строят Х+ и если Y Í Х+, то значит XàY Í F+.
Основная задача заключается в построении алгоритма замыкания множества атрибутов.
Алгоритм построения замыкания множества атрибутов.
Это итерационная процедура, включающая следующие шаги:
- i:=0, X0+=X – замыкание множества атрибутов на i-ом шаге.
- Положить X+i+1:= X+iÈV, где V – множеств атрибутов такое, что в F имеется функциональная зависимость Y→Z, для которых YÍ X+i , а VÍZ.
- X+i+1= X+i – это есть X+:= X+i , иначе i:=i+1 и перейти к шагу 2.
Пример замыкания множества атрибутов.
R=(A,B,C,D,E,G),
F=(AB→C, C→A, BC→D. ACD→B, D→EG, BE→C, CG→BD, CE→AG)
X=BD, X+ - ?
- X0+≔BD
- и 3. Оформим в виде таблицы:
| i | Y→Z, для которых YÍ X+i | VÍZ | X+i+1≔ X+iÈV |
| D→EG | EG | EGBD X+1 | |
| BE→C | C | EGBDC X+2 | |
| C→A, BC→D, CG→BD, CE→AG | A | EGBDCA X+3 | |
| AB→C, ACD→B | EGBDCA X+4 |
Т.о. (BD)+ = EGBDCA *Þ
(BD→E, BD→G, BD→B, BD→C, BD→D, BD→A) Ì F+ **
* и ** эквивалентны.
2. Методы индексации данных, используемые в СУБД (хеш-индекс, B-деревья).
Методы индексации данных в реляционных СУБД
Индекс – это некоторая структура, обеспечивающая быстрый поиск данных в БД.
Различают следующие типы Индексов:
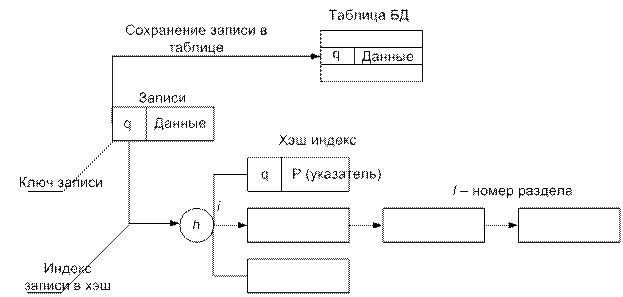
- Хэш – индекс
- B – индекс
Дата добавления: 2015-04-21; просмотров: 716; Мы поможем в написании вашей работы!; Нарушение авторских прав |