
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Машинное представление графов
Существуют два основных метода представления графов в памяти: матричный (массивами), и связными нелинейными списками. Выбор метода зависит от природы данных и операций, выполняемых над ними. Если задача требует большого числа включений и исключений узлов, то целесообразно представлять граф связными списками. В противном случае можно применить и матричное представление.
При представлении в виде списочной структуры, используется два типа списков - список вершин и список ребер. Элемент списка вершин содержит поле данных и два указателя. Один указатель связывает данный элемент с элементом другой вершины. Второй указатель связывает элемент списка вершин со списком ребер, связанных с данной вершиной.
Для ориентированного графа используют список дуг, исходящих из вершины (рис. 6.3). Элемент списка дуг состоит только из двух указателей. Первый указатель используется для того, чтобы показать в какую вершину дуга входит, а второй - для связи элементов в списке дуг вершины.

а).
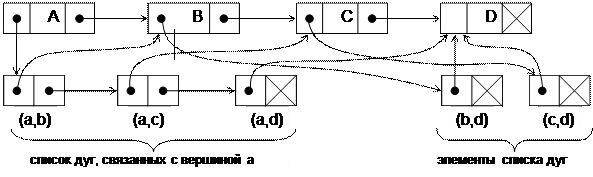
б).
Рис. 6.3. Представление графа (а) в виде списочной структуры (б).
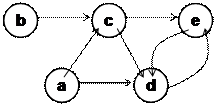
Распространенным способом представления графов является матричный способ (рис. 6.4). Для ненаправленных графов обычно используют матрицы смежности, а для ориентированных графов - матрицы инцидентности. Обе матрицы имеют размерность n*n, где n-число вершин в графе.
При использовании матриц смежности их элементы представляются в памяти элементами массива. Элемент матрицы имеет ноль в позиции m(i,j), если не существует ребра, связывающего вершину i с вершиной j, или имеет единичное значение в позиции m(i,j), если такое ребро существует. Матрицы смежности применяются, когда в графе много связей и матрица хорошо заполнена.
Для простого графа матрица состоит из нулей и единиц, для мультиграфа - из нулей и целых чисел, указывающих кратность соответствующих ребер, для взвешенного графа - из нулей и вещественных чисел, задающих вес каждого ребра.
Матрица смежности симметрична относительно главной диагонали, поэтому можно хранить и обрабатывать только часть матрицы. Для хранения одного элемента матрицы достаточно выделить всего один бит.
 |
Матрица смежности.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица инцидентности.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Рис. 6.4. Граф и его матричное представление.
Правила построения матрицы инцидентности аналогичны правилам построения матрицы инцидентности. Разница состоит в том, что единица в позиции m(i,j) означает выход дуги из вершины i и вход дуги в вершину j.
В некоторых матричных алгоритмах обработки графов используются матрицы путей. Под путем длиной k из вершины i в вершину j будем понимать возможность попасть из вершины i в вершину j за k переходов, каждому из которых соответствует одна дуга. Одна матрица путей mk содержит сведения о наличии всех путей одной длины k в графе. Единичное значение в позиции (i,j) означает наличие пути длины k из вершины i в вершину j.
Матрица m1 полностью совпадает с матрицей инцидентности. По матрице m1 можно построить m2 , а по матрице m2 можно построить m3 и т.д. Если граф является ациклическим, то число матриц путей ограничено. В противном случае матрицы будут повторяться до бесконечности с некоторым периодом, связанным с длиной циклов. Матрицы путей не имеет смысла вычислять до бесконечности. Достаточно остановиться в случае повторения матриц.
Матрица путей m1.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица путей m2.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
Матрица путей m3.
| a | b | c | d | e | |
| a | |||||
| b | |||||
| c | |||||
| d | |||||
| e |
2. Общая схема симметричной криптосистемы. Алгоритм построения цепочек.
Дата добавления: 2015-04-21; просмотров: 486; Мы поможем в написании вашей работы!; Нарушение авторских прав |