Билет 4.

1. Нормальный алгоритм Маркова.

Норма́льный алгори́тм Ма́ркова (НАМ) — один из стандартных способов формального определения понятия алгоритма. Понятие нормального алгоритма введено А. А. Марковым в конце 1940-х годов. Традиционно, когда говорят об алгоритмах Маркова, используют слово «алгорифм».

Нормальный алгоритм описывает метод переписывания строк, похожий по способу задания на формальные грамматики. НАМ является Тьюринг-полным языком, что делает его по выразительной силе эквивалентным машине Тьюринга и следовательно современным языкам программирования. ( про машину Тьюринга лучше не упоминать, чтобы не было дополнительных вопросов, но в курсе дела надо быть).

На основе НАМ был создан функциональный язык программирования Рефал.

Нормальные алгоритмы являются вербальными, то есть предназначенными для применения к словам в различных алфавитах. Определение всякого нормального алгоритма состоит из двух частей: определения алфавита алгоритма (к словам из символов которого алгоритм будет применяться) и определения его схемы. Схемой нормального алгоритма называется конечный упорядоченный набор т. н. формул подстановки, каждая из которых может быть простой или заключительной. Простыми формулами подстановки называются слова вида , где L и D — два произвольных слова в алфавите алгоритма (называемые, соответственно, левой и правой частями формулы подстановки). Аналогично, заключительными формулами подстановки называются слова вида 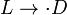, где L и D — два произвольных слова в алфавите алгоритма. При этом предполагается, что вспомогательные буквы и 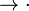не принадлежат алфавиту алгоритма (в противном случае на исполняемую ими роль разделителя левой и правой частей следует избрать другие две буквы).

Примером схемы нормального алгоритма в пятибуквенном алфавите | * abc может служить схема

Процесс применения нормального алгоритма к произвольному слову V в алфавите этого алгорифма представляет собой дискретную последовательность элементарных шагов, состоящих в следующем. Пусть V' — слово, полученное на предыдущем шаге работы алгорифма (или исходное слово V, если текущий шаг является первым). Если среди формул подстановки нет такой, левая часть которой входила бы в V', то работа алгоритма считается завершённой, и результатом этой работы считается слово V'. Иначе среди формул подстановки, левая часть которых входит в V', выбирается самая верхняя. Если эта формула подстановки имеет вид 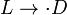, то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего работа алгоритма считается завершённой с результатом RDS. Если же эта формула подстановки имеет вид , то из всех возможных представлений слова V' в виде RLS выбирается такое, при котором R — самое короткое, после чего слово RDSсчитается результатом текущего шага, подлежащим дальнейшей переработке на следующем шаге.

Например, в ходе процесса применения алгорифма с указанной выше схемой к слову | * | | последовательно возникают слова | b * | , ba | * | , a | * | , a | b * , aba | * , baa | * , aa | * ,aa | c, aac, ac | и c | | , после чего алгорифм завершает работу с результатом | | . Другие примеры смотрите ниже.

Нормальные алгорифмы оказались удобным средством для построения многих разделов конструктивной математики. Кроме того, заложенные в определении нормального алгорифма идеи используются в ряде ориентированных на обработку символьной информации языков программирования — например, в языке Рефал.

Пример

Данный алгоритм преобразует двоичные числа в «единичные», то есть на выходе получается строка из N единичек, если на входе у нас было N в двоичной системе. Например, 101 преобразуется в 5 единиц:

Правила:

«|0» → "0||"

«1» → "0|"

«0» → "" (пустая строка)

Исходная строка:

«101»

Выполнение:

«0|01»

«00||1»

"00||0|"

"00|0