Применение бинарных деревьев для сжатия информации

Бинарные деревья применяются в задачах сжатия информации. Рассмотрим пример. Имеется текстовая строка S, состоящая из 10 символов S = ABCCCDDDDD. При кодировании одного символа одним байтом для строки потребуется 10 байт. Попробуем сократить требуемую память. Рассмотрим, какие символы действительно требуется кодировать. В данной строке используются всего 4 символа. Поэтому можно использовать укороченный код.

A 00

B 01

C 10

D 11

b = 00011010101111111111 (20 бит)

В данном случае мы проанализировали текст на предмет использования символов. Можно заметить, что различные символы имеют различную частоту повторения. Существующие методы кодирования позволяют использовать этот факт для уменьшения длины кода. Одним из таких методов является кодирование Хаффмана. Он основан на использовании кодов различной длины для различных символов. Для максимально повторяющихся символов используют коды минимальной длины.

Построение кодовой таблицы происходит с использованием бинарного дерева (рис. 6.20). В корне дерева помещаются все символы и их суммарная частота повторения. Далее выбирается наиболее часто используемый символ и помещается со своей частотой повторения в левое поддерево. В правое поддерево помещаются оставшиеся символы с их суммарной частотой. Затем описанная операция проводится для всех вершин дерева, которые содержат более одного символа.

Само дерево может быть использовано в качестве кодовой таблицы для кодирования и декодирования текста. Кодирование осуществляется следующим образом. Для очередного символа в качестве кода используется путь от листа соответствующего символа к корню дерева. Причем каждому левому поддереву приписывается ноль, а каждому правому - единица.

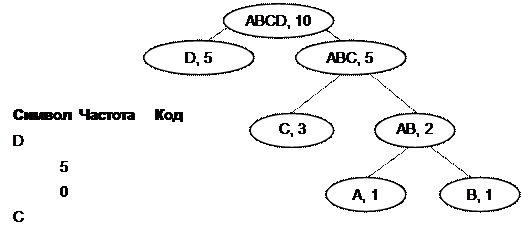
Рис. 6.20. Построение кодовой таблицы.

Для строки S будет получен следующий код b=11011110101000000. Длина кода составляет 17 бит, что меньше по сравнению с укороченным кодом. Алгоритм распаковки можно сформулировать следующим образом:

1. i:=0, j:=0;

2. если i > n, то стоп строка распакована, иначе i:=i+1;

3. node:= root;

4. если b(i) = 0, то node:=left(node), иначе node:=right(node)

5. если left(node) = 0 и right(node) = 0, то j:=j+1, s(j):= str(node),

перейти к шагу 2, иначе i:=i+1, перейти к шагу 4

В алгоритме корень дерева обозначен как root, а left(node) и right(node) обозначают левый и правый потомки узла node.

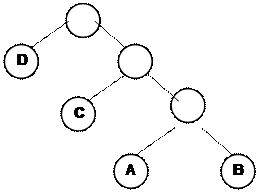
На практике такие способы упаковки используются не только для текстов, но и для произвольных двоичных данных. Любой файл можно рассматривать как последовательность байт. Тогда дерево кодирования можно построить не для символов, а для значений байт, встречающихся в кодируемом файле (рис. 6.21). Поскольку байт может принимать 256 значений, то соответствующее дерево будет иметь не более 256 листьев.

	строка S

Рис. 6.21. Процесс распаковки кода.

В узлах дерева после его полного построения нет необходимости хранить несколько значений кодов и частоты повторения. Для кодирования и декодирования достаточно хранить только одно значение кода и только для листового узла. Поэтому такой способ представления кодовой таблицы является достаточно компактным. Схемы кодирования подобного типа используются в программах архивации данных и сжатия растровых изображений в форматах графических файлов.