
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Применение ЭКД в физической химии и металлургии
Использование ЭКД для решения теоретических и прикладных вопросов металлургии представляется очень перспективным. Физико-химический аспект изучения ЭКД связан прежде всего с тем, что скорость движения зависит от вида электрокапиллярной кривой (от величины ds12/dφ), а направление – от знака этой производной, т.е. от знака поверхности металла. Изучая зависимость скорости ЭКД от Е и r, удается, следовательно, определить знак и оценить величину заряда.
В металлургии: повышение интенсивности конвекции при помощи ЭКД является эффективным способом улучшения качества металлав заводских условиях, например, процесс капельного шлакового рафинирования сталей и сплавов. Здесь металл по каплям проходит через слой шлака. Это позволяет повысить степень его очистки от вредных примесей, поскольку большая удельная поверхность капли и развитая конвекция способствуют ускорению их перхода в шлаковую фазу. Также извлечение ценных металлов из шлаков возможно за счет ЭКД, т.к. разность плотностей металла и шлака обуславливают повышенную скорость оседания капель металла. С помощью ЭКД замедляют оседание капель металла в жидком шлаке: капли металла, проходя через шлак очень быстро очищаются от вредных примесей («электрошлаковый переплав») – сверхдорогая технология. Также осуществляется уменьшение размера образования капель с помощью ЭКД. Под влиянием ЭКД капля как бы срезается с капилляра до того, как ее вес станет достаточным для отрыва под действием гравитационных сил.
Для чего используется графический метод кинетического анализа реакций между металлом и шлаком? Поясните сущность метода. Какие данные необходимы для того, чтобы этим методом оценить влияние температуры, концентрации реагентов, интенсивности конвективных потоков на скорость перехода заданного элемента через границу фаз? (288-297) Попель
Графический метод расчета скорости реакции
рассмотрим в качестве примера кинетику реакции
(Fe2+) + (О2-) = [Fe] + [О], (VII.93)
протекающей на границе металла с оксидным расплавом в сталеплавильных агрегатах. Будем считать, что электродные процессы (О2-) =[O]+2е; [Fe]= (Fe2+) +2е, совокупность которых составляет реакцию (VII.93), изучены. В частности, известны вольтамперные характеристики  = =f(η0) и
= =f(η0) и  f(ηFe2+ ), анализ которых показал, что в рассматриваемых условиях величина
f(ηFe2+ ), анализ которых показал, что в рассматриваемых условиях величина  лимитируется электрохимической, a
лимитируется электрохимической, a  — диффузионной стадией. Во втором случае заторможенной является диффузия ионов (Fe2+) в прилегающем к металлу слое оксидной фазы. Нанесем обе вольтамперные характеристики на график, построенный в координатах i — φ
— диффузионной стадией. Во втором случае заторможенной является диффузия ионов (Fe2+) в прилегающем к металлу слое оксидной фазы. Нанесем обе вольтамперные характеристики на график, построенный в координатах i — φ  (рис. VII.3), где φ — электродный потенциал, измеренный относительно какого-либо электрода сравнения. При построении графика необходимо на оси потенциалов отметить для каждого процесса значение φ, при котором η, а значит,
(рис. VII.3), где φ — электродный потенциал, измеренный относительно какого-либо электрода сравнения. При построении графика необходимо на оси потенциалов отметить для каждого процесса значение φ, при котором η, а значит,
и i равны нулю. Эти потенциалы, называемые равновесными, определяются обычными термодинамическими соотношениями:

В реальной взаимодействующей системе без внешнего источника тока
 (VII.96)
(VII.96)
Согласно диаграмме рис. VII.3, условие (VII.96) может быть выполнено только при установлении на границе фаз потенциала, обозначенного на диаграмме символом  и называемого компромиссным или стационарным. При φ=
и называемого компромиссным или стационарным. При φ=  скорости электродных процессов в электрических единицах равны по абсолютной величине и противоположны по знаку. Процесс, для которого равновесный потенциал более отрицателен (в данном случае процесс с участием кислорода), протекает в положительном (анодном) направлении (i > 0). Компромиссный потенциал всегда находится между равновесными, часто приближаясь к одному из них. Положение
скорости электродных процессов в электрических единицах равны по абсолютной величине и противоположны по знаку. Процесс, для которого равновесный потенциал более отрицателен (в данном случае процесс с участием кислорода), протекает в положительном (анодном) направлении (i > 0). Компромиссный потенциал всегда находится между равновесными, часто приближаясь к одному из них. Положение  по оси абсцисс позволяет выявить природу наиболее замедленной стадии. Если φ≈
по оси абсцисс позволяет выявить природу наиболее замедленной стадии. Если φ≈  то стадией, лимитирующей скорость, является окисление ионов О2-, в то время как восстановление Fe2+ протекает с малым перенапряжением.
то стадией, лимитирующей скорость, является окисление ионов О2-, в то время как восстановление Fe2+ протекает с малым перенапряжением.
Таким образом, построив диаграмму i—φ, можно определить скорость реакции (VII.93):
 =
=  (VII.97)
(VII.97)
воспользовавшись для этого значением плотности тока  , соответствующим компромиссному потенциалу. Очевидно, что для построения не обязательно знать значения равновесных потенциалов
, соответствующим компромиссному потенциалу. Очевидно, что для построения не обязательно знать значения равновесных потенциалов  и
и  , измеренных относительно одного и того же электрода сравнения, достаточно знать разность
, измеренных относительно одного и того же электрода сравнения, достаточно знать разность  —
—  .
.
Для знакомства с методикой расчета разности равновесных потенциалов продолжим рассмотрение реакции (VI 1.93), а затем обобщим полученный результат. Согласно выражениям (VII.94) и (VII.95):
 -
-  =
=  -
- 
 (VII.98)
(VII.98)
Запишем соотношение (VI 1.98) для той же температуры и таких концентраций реагентов, при которых реакция (VII.93) находится в равновесии, т. е.  ~
~  =0. В этих условиях
=0. В этих условиях  =
=  , а под знаком логарифма находится величина, равная константе равновесия рассматриваемой реакции. Следовательно,
, а под знаком логарифма находится величина, равная константе равновесия рассматриваемой реакции. Следовательно,  —
— 
 а искомая разность равновесных потенциалов
а искомая разность равновесных потенциалов
определяется разностью между логарифмами фактического и равновесного произведений активности реагентов:
(VII. 99)
c(FeO)
Сравнивая соотношение (VII.99) с уравнением изотермы химической реакции (VII.93), находим, что
 -
-  , (VII. 100)
, (VII. 100)
где ∆G — изменение энергии Гиббса при образовании одного моля [О]. В общем случае
 (VII .101)
(VII .101)
Где 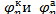 — равновесные потенциалы для электродных процессов, протекающих в катодном и анодном направлениях соответственно; zF—количество электричества, перешедшего от восстановителя к окислителю при образовании такого количества продуктов реакции, для которого рассчитана величина ∆G.
— равновесные потенциалы для электродных процессов, протекающих в катодном и анодном направлениях соответственно; zF—количество электричества, перешедшего от восстановителя к окислителю при образовании такого количества продуктов реакции, для которого рассчитана величина ∆G.
При помощи диаграммы i—φ можно изучить влияние различных факторов на скорость реакции и ее режим, для этого необходимо учесть, как изменились разность равновесных потенциалов и ход каждой вольтамперной характеристики под действием этих факторов.
При повышении температуры увеличивается крутизна вольтамперных характеристик при любом режиме электродных процессов, так как предельные токи диффузии, токи ионного обмена, константы скорости увеличиваются с температурой. Кроме того, температура влияет и на разность равновесных потенциалов. Если, например, при постоянных концентрациях реагентов повышение температуры вызвало рост неравновесности системы (величина ∆G стала более отрицательной), то, согласно уравнению (VII. 101), это приведет к увеличению разности  , что в свою очередь влияет на скорость реакции. Таким образом, влияние температуры на скорость реакции обусловлено температурной зависимостью кинетических характеристик электродных процессов и величины ∆G, определяющей разность равновесных потенциалов.
, что в свою очередь влияет на скорость реакции. Таким образом, влияние температуры на скорость реакции обусловлено температурной зависимостью кинетических характеристик электродных процессов и величины ∆G, определяющей разность равновесных потенциалов.
При помощи диаграммы i—φ можно изучить влияние различных факторов на скорость реакции и ее режим, для этого необходимо учесть, как изменились разность равновесных потенциалов и ход каждой вольтамперной характеристики под действием этих факторов.
При повышении температуры увеличивается крутизна вольтамперных характеристик при любом режиме электродных процессов, так как предельные токи диффузии, токи ионного обмена, константы скорости увеличиваются с температурой. Кроме того, температура влияет и на разность равновесных потенциалов. Если, например, при постоянных концентрациях реагентов повышение температуры вызвало рост неравновесности системы (величина ∆G стала более отрицательной), то, согласно уравнению (VII. 101), это приведет к увеличению разности  , что в свою очередь влияет на скорость реакции. Таким образом, влияние температуры на скорость реакции обусловлено температурной зависимостью кинетических характеристик электродных процессов и величины ∆G, определяющей разность равновесных потенциалов.
, что в свою очередь влияет на скорость реакции. Таким образом, влияние температуры на скорость реакции обусловлено температурной зависимостью кинетических характеристик электродных процессов и величины ∆G, определяющей разность равновесных потенциалов.
Влияние концентрации реагентов на скорость взаимодействия может быть сравнительно сложным. Кажущийся порядок реакции зависит от того, в каком режиме протекают электродные процессы и в какой мере каждый из них определяет скорость реакции в целом. Для пояснения сказанного рассмотрим частные случаи.
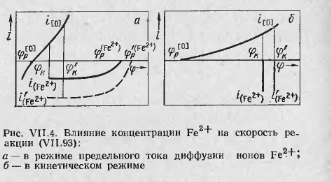
1. Если в шлаковой фазе слабо развиты конвективные потоки, вольтамперная характеристика электродного процесса с участием ионов железа, протекающего в диффузионном режиме, окажется пологой, а компромиссный потенциал—близким к равновесному по кислороду (рис. VI 1.4, а). При достаточно большой разности равновесных потенциалов это приведет к тому, что плотность тока катодного восстановления ионов (Fe2+), а следовательно, и скорость реакции (VI 1.93) в электрических единицах станут близки к предельному току  . В данном случае лимитирующим звеном процесса является диффузия ионов двухвалентного железа, причем их концентрация у границы фаз близка к нулю. Обмен ионами кислорода протекает в квазиравновесных условиях (
. В данном случае лимитирующим звеном процесса является диффузия ионов двухвалентного железа, причем их концентрация у границы фаз близка к нулю. Обмен ионами кислорода протекает в квазиравновесных условиях (  ). Поскольку предельный ток диффузии прямо пропорционален концентрации диффундирующих частиц, то реакция (VII.93) имеет первый порядок. Действительно, рассмотрим, как изменится диаграмма i—φ при увеличении концентрации (Fe2+) в два раза. Во-первых, такое увеличение в соответствии с законами диффузионной кинетики вызовет рост крутизны вольтамперной характеристики катодного процесса и увеличение
). Поскольку предельный ток диффузии прямо пропорционален концентрации диффундирующих частиц, то реакция (VII.93) имеет первый порядок. Действительно, рассмотрим, как изменится диаграмма i—φ при увеличении концентрации (Fe2+) в два раза. Во-первых, такое увеличение в соответствии с законами диффузионной кинетики вызовет рост крутизны вольтамперной характеристики катодного процесса и увеличение  в два раза (см. пунктирную кривую на рис. VII.4,а). Во-вторых, равновесный потенциал несколько сместится в сторону более положительных значений [см. уравнение (VII.95)]. Однако, как видно из рис. VII.4, а, смещение равновесногопотенциала практически не влияет на скорость взаимодействия при новом компромиссном потенциале фк, если справедливо равенство
в два раза (см. пунктирную кривую на рис. VII.4,а). Во-вторых, равновесный потенциал несколько сместится в сторону более положительных значений [см. уравнение (VII.95)]. Однако, как видно из рис. VII.4, а, смещение равновесногопотенциала практически не влияет на скорость взаимодействия при новом компромиссном потенциале фк, если справедливо равенство 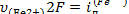

| Рис. VII.5. Влияние интенсивности конвективных потоков со на скорость реакции (VI 1.93), притекающей в смешанном режиме |
2. Диаграмма i—φ для случая, обратного рассмотренному выше, приведена на рис. VII.4, б. Пологой является вольтамперная характеристика анодного процесса, в то время как для катодного она настолько крута (практически вертикальна), что компромиссный потенциал совпадает с равновесным  ≈
≈  Ясно, что в этих условиях единственной причиной роста скорости взаимодействия при увеличении содержания (Fe2+) является смещение равновесного потенциала для катодного процесса (сравните φк и φк). Логарифмический закон смещения (VI1.95) обусловливает более сложную по сравнению с предыдущим случаем концентрационную зависимость скорости реакции. При значительных удалениях реакции (VII.93) от равновесия ее порядок оказывается дробным, а при малых удалениях
Ясно, что в этих условиях единственной причиной роста скорости взаимодействия при увеличении содержания (Fe2+) является смещение равновесного потенциала для катодного процесса (сравните φк и φк). Логарифмический закон смещения (VI1.95) обусловливает более сложную по сравнению с предыдущим случаем концентрационную зависимость скорости реакции. При значительных удалениях реакции (VII.93) от равновесия ее порядок оказывается дробным, а при малых удалениях  ~ (—∆G)
~ (—∆G)
Влияние интенсивности конвективных потоков на скорость взаимодействия оказывается простым, если оба электродных процесса протекают в одинаковом режиме. Если режим кинетический, то такое влияние отсутствует, если — диффузионный, то скорость каждого электродного процесса, а значит, и реакции прямо пропорциональна квадратному корню из скорости ламинарных потоков. Остановимся на более сложном случае, когда режим электродных процессов различен. Рассмотрим, например, реакцию (VII.93), протекающую в условиях регулируемой конвекции на границе жидких фаз, перемешиваемых какой-либо мешалкой с угловой скоростью вращения ω. Равновесные потенциалы катодного и анодного процессов определяются содержанием реагентов в объеме фаз и не зависят от ω. Рост интенсивности перемешивания не влияет также на ход вольтамперной характеристики анодного окисления ионов О2-, протекающего в данном случае в кинетическом режиме. Катодная стадия (восстановление Fe2+ до Fe) протекает в диффузионном режиме, следовательно, при постоянном перенапряжении  . На рис. VII.5 приведена диаграмма i — φ, иллюстрирующая влияние ω на скорость рассматриваемой реакции. Поляризационные кривые катодного процесса соответствуют трем различным значениям о, причем
. На рис. VII.5 приведена диаграмма i — φ, иллюстрирующая влияние ω на скорость рассматриваемой реакции. Поляризационные кривые катодного процесса соответствуют трем различным значениям о, причем  , т. е. при постоянном катодном перенапряжении (при постоянном отклонении φ от
, т. е. при постоянном катодном перенапряжении (при постоянном отклонении φ от  скорость восстановления Fe2+ возрастает в два раза при переходе от
скорость восстановления Fe2+ возрастает в два раза при переходе от  к
к  и от
и от  к
к  Как следует из рис. VI 1.5, увеличение скорости вращения мешалки приводит к смещению компромиссного потенциала в положительном направлении. Одновременно увеличивается скорость реакции (VII.93), однако темп увеличения
Как следует из рис. VI 1.5, увеличение скорости вращения мешалки приводит к смещению компромиссного потенциала в положительном направлении. Одновременно увеличивается скорость реакции (VII.93), однако темп увеличения  с ростом ω не остается постоянным. Так, при скоростях вращения
с ростом ω не остается постоянным. Так, при скоростях вращения  и
и  скорость реакции в электрических единицах практически равна предельному току диффузии Fe2+, поэтому
скорость реакции в электрических единицах практически равна предельному току диффузии Fe2+, поэтому 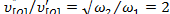 . При дальнейшем увеличении ω до
. При дальнейшем увеличении ω до  величина
величина  2F оказывается существенно меньше предельного тока диффузии Fe2+ и соответственно
2F оказывается существенно меньше предельного тока диффузии Fe2+ и соответственно  . Это свидетельствует о переходе реакции (VII.93) в смешанный режим, т. е. о возрастании кинетических торможений анодного процесса. Согласно диаграмме i—φ, при ω→∞ будет достигнуто некоторое предельное значение скорости, характерное для кинетического режима взаимодействия. Это значение можно найти, поскольку при ω→∞ компромиссный потенциал совпадает с
. Это свидетельствует о переходе реакции (VII.93) в смешанный режим, т. е. о возрастании кинетических торможений анодного процесса. Согласно диаграмме i—φ, при ω→∞ будет достигнуто некоторое предельное значение скорости, характерное для кинетического режима взаимодействия. Это значение можно найти, поскольку при ω→∞ компромиссный потенциал совпадает с  Сказанное справедливо лишь в том случае, если режим катодного процесса остается диффузионным и при больших значениях ω.
Сказанное справедливо лишь в том случае, если режим катодного процесса остается диффузионным и при больших значениях ω.
Дата добавления: 2015-04-18; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |