
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПОЛИМЕРНАЯ МОДЕЛЬ БИНАРНЫХ СИЛИКАТНЫХ РАСПЛАВОВ, УЧИТЫВАЮЩАЯ ПЕРЕМЕННУЮ ФУНКЦИОНАЛЬНОСТЬ МОНОМЕРА
Попытаемся получить уравнения, позволяющие сравнительно просто рассчитывать структурные характеристики силикатных расплавов во всем интервале их составов. Учтем наличие кольцевых ионов. Допустим, что мономер  является бифункциональным (f = 2) в цепных анионах (включая и отдельные тетраэдры) и тетрафункциональным (f = 4) в кольцевых. Это допущение основывается на экспериментальныхданных, свидетельствующих об отсутствии разветвленных цепей в силикатных расплавах. В линейных же цепях всегда равна 2, то есть, только 2 из 4 концевых атомов кислорода в кремнекислородном тетраэдре реакционно способны.
является бифункциональным (f = 2) в цепных анионах (включая и отдельные тетраэдры) и тетрафункциональным (f = 4) в кольцевых. Это допущение основывается на экспериментальныхданных, свидетельствующих об отсутствии разветвленных цепей в силикатных расплавах. В линейных же цепях всегда равна 2, то есть, только 2 из 4 концевых атомов кислорода в кремнекислородном тетраэдре реакционно способны.
Содержание кольцевых анионов увеличивается с повышением степени полимеризации, поэтому можно говорить о переменной среддней функциональности мономера, которая изменяется от 2 (в полностью деполимеризованном расплаве) до 4 (в чистом  ). Это повышение функциональности происходит постепенно, по мере увеличения степени полимеризации α.
). Это повышение функциональности происходит постепенно, по мере увеличения степени полимеризации α.
В, полностью деполимеризованном, расплаве при f=2, содержится  функциональных кольцевых атомов кислорода
функциональных кольцевых атомов кислорода  (функциональных групп). За счёт тетрафункциональности мономера в кольцевых анионах появляются дополнительно
(функциональных групп). За счёт тетрафункциональности мономера в кольцевых анионах появляются дополнительно  , функциональных групп, которые расходуются в реакциях замыкания между кольцевыми анионами. Согласно реакции поликонденсации, записанной в общем виде:
, функциональных групп, которые расходуются в реакциях замыкания между кольцевыми анионами. Согласно реакции поликонденсации, записанной в общем виде:
 (i – 1 + c)
(i – 1 + c) 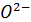 , (1)
, (1)
В одном моле расплава из 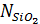 тетраэдров
тетраэдров  образуется с учётом только плоских колец (число самозамыканий с = 1)
образуется с учётом только плоских колец (число самозамыканий с = 1) 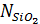 ионов
ионов 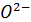 , при i→c→∞ имеем
, при i→c→∞ имеем  ионов
ионов 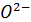 . Тогда максимальное число ионов
. Тогда максимальное число ионов 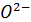 , которые могут появится в результате протекания всех возможных реакций замыкания колец, будет равно
, которые могут появится в результате протекания всех возможных реакций замыкания колец, будет равно 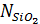 , или в общем случае
, или в общем случае  . Столько же появится и мостиковых атомов кислорода
. Столько же появится и мостиковых атомов кислорода  . Таким образом, дополнительные функциональные группы расходуются нацело. В итоге, при учёте распределения всех
. Таким образом, дополнительные функциональные группы расходуются нацело. В итоге, при учёте распределения всех  +
+  , функциональных групп число молей соответствующих форм кислорода в моле полимеризованного расплава MeO – SiO2 (
, функциональных групп число молей соответствующих форм кислорода в моле полимеризованного расплава MeO – SiO2 (  составит:
составит:
 (2)
(2)
 , (3)
, (3)
 (4)
(4)
В дальнейшем будем полагать, что все функциональные кольцевые атомы кислорода обладают одинаковой реакционной способностью.
Кроме этих форм кислорода, в расплаве, также, присутствуют нефункциональные, которые не участвуют в реакции поликонденсации, но должны учитываться при составлении баланса по кислороду. Число молей таких нефункциональных концевых атомов кислорода равно:
 =
= 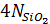 -
-  +
+  ) =
) =  (1 – α), (5)
(1 – α), (5)
Заметим, что полное использование дополнительных функциональных групп предполагает, что появляющиеся плоские кольца сразу же взаимодействуют друг с другом, образуя сложные объемные (i → с) структуры. Это должно ограничивать размеры линейных и плоских кольцевых форм. Именно об этом свидетельствуют рассмотренные выше экспериментальные данные.
Отсутствие в силикатных расплавах изомерных форм анионов позволяет допустить, что реакции взаимодействия кольцевых анионов описываются теми же уравнениями линейной поликонденсации, что и цепных анионов. Действительно, в случае i → с применение формулы Бернулли приводит к тому же выражению для константы равновесия реакции (1), что и в случае линейной поликонденсации:
 (6)
(6)
Ионную долю «свободных» ионов кислорода 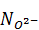 найдем по формуле
найдем по формуле
 (7)
(7)
Общее число молей силикатных анионов в моле расплава выразим как:
 =
=  =
=  (1 - α) (8)
(1 - α) (8)
Здесь  = 1/(1 — а) —среднее число тетраэдров, приходящихся на один силикатный анион.
= 1/(1 — а) —среднее число тетраэдров, приходящихся на один силикатный анион.
В итоге, получаем

41. Используя бесструктурную модель оксидных расплавов, выведите уравнение, описывающее константу полимеризации шлака. (см. Климов 98%) (см. лекции Климов 62)
42. Используя структурную модель полимеризации оксидных расплавов, выведите формулу, описывающую константу полимеризации шлака. (см. Климов 98%) (см. лекции Климов 62)
43. Используя структурную модель полимеризации расплавов, выведите формулу, позволяющую оценивать активность компонентов шлака. (см. Климов 98%)
Рассмотрите эволюцию взглядов на природу шлаков и современные представления о структуре расплавленных шлаков. Обоснуйте, базируясь на экспериментальных данных, ионное строение кристаллических силикатов и оксидных расплавов. Опишите структурные составляющие шлаков: одноатомные и многоатомные катионы и анионы. (см. Климов 98%) (см. лекции Климов1 25-44) Лена Ирдуганова знает ответ на полимерную модель!!!
45. Опишите процесс формирования полимеризованных анионов: кремнекислородных, фосфорокислородных, алюмокислородных и т. д. Объясните типы химической связи в полимеризованных анионах. Рассмотрите влияние природы катиона на состав полимеризованных анионов. (см. Климов 98%)(34-38) Артамонова (см. лекции Климов 45)
Осуществите термодинамический анализ процессов растворения газообразных водорода, азота, серы, фосфора, кислорода, моно- и диоксида углерода в металлах. Рассмотрите факторы, определяющие растворимость газов в металлах: температура, давление, агрегатное состояние металла и его природа, наличие в металле примесей и легирующих элементов и др.
Содержание газов в металле в большинстве случаев отрицательно влияет на свойства готовых изделий. Знание процессов растворения газов в металле и факторов, влияющих на поведение газов в жидких металле, позволяет выработать правильные технологические приемы выплавки стали и сплавов с низким содержанием газов.
Для определения растворимости газов используют метод Сивертса. Если газы образуют в металле раствор, подчиняющийся закону Генри, то равновесная концентрация двухатомных газов (H2, O2, N2) пропорциональна корню квадратному из парциального давления газа над металлом
 – газ в металле
– газ в металле
 (1)
(1)
Эта зависимость является диссоциация двухатомных молекул 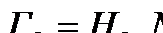 на атомы. Равновесие компонента в газовой фазе и растворенного в металле в этом случае можно записать
на атомы. Равновесие компонента в газовой фазе и растворенного в металле в этом случае можно записать
 (2)
(2)
Константа равновесия
 (3)
(3)
При не очень высоких давлениях активность компонента газовой фазы  численно равна его парциальному давлению
численно равна его парциальному давлению  , выраженному в атмосферах (
, выраженному в атмосферах (  =1), а растворы водорода и азота в железе разбавленными, вследствие чего их активности пропорциональны концентрациям
=1), а растворы водорода и азота в железе разбавленными, вследствие чего их активности пропорциональны концентрациям  . Объединяя постоянные величины
. Объединяя постоянные величины 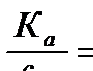 , получим уравнение (1).
, получим уравнение (1).
Равновесная концентрация газа в металле при  =1 ат. (0,1 МПа) называется его растворимостью и численно равна константе равновесия в уравнении (1).
=1 ат. (0,1 МПа) называется его растворимостью и численно равна константе равновесия в уравнении (1).
Изменение растворимости водорода и азота в железе с температурой иллюстрирует рисунок 1.
| Т, К |
| [H], [N], % |
| 0,01 |
| 0,02 |
| 0,03 |
| 0,04 |
| 0,05 |
| α-Fe |
| γ-Fe |
| δ-Fe |
| Feж |
| [N] |
| [H] |
Рисунок 1.
Растворимость обоих газов с повышением температуры возрастает как в твердом, так и в жидком железе, что свидетельствует об эндотермичности процессов (  ,
,  ,
,  , следовательно,
, следовательно,  т.е. функция возрастает).
т.е. функция возрастает).
Исключение составляет только растворимость азота в γ-Fe, которая уменьшается с возрастанием температуры. В точках фазовых переходов из одной модификации в другую и при плавлении равновесные концентрации газов в растворе претерпевают скачкообразные изменения. Количественно изменения констант равновесия К, а следовательно, и растворимостей газов при изменении температуры можно определить, интегрируя уравнение изобары химической реакции
 , (4)
, (4)
где  – теплота растворения соответствующего газа в чистом металле, зависящая от температуры. Однако обычно более точные значения констант равновесия получают по эмпирическим уравнениям. Для водорода с жидким железом
– теплота растворения соответствующего газа в чистом металле, зависящая от температуры. Однако обычно более точные значения констант равновесия получают по эмпирическим уравнениям. Для водорода с жидким железом
 , (5)
, (5)
а для азота
 . (6)
. (6)
В соответствии с этими уравнениями при 1873 К растворимость водорода в железе составляет 29 см3/100г, или 2,6*10-3%, а азота соответственно 16 см3/100г, или 4,4*10-2.
При равновесии отдельного газа с железом по реакции (2) система является двухкомпонентной (k=2) и двухфазной (Ф=2), поэтому число степеней свободы
 (7)
(7)
Из трех переменных, определяющих состояние системы (  , Т,
, Т,  ), в условиях равновесия независимы две. Если в качестве независимых выбрать
), в условиях равновесия независимы две. Если в качестве независимых выбрать  и Т, как более легко определяемые экспериментально, то равновесная концентрация газа будет зависеть от температуры и давления, т.е.
и Т, как более легко определяемые экспериментально, то равновесная концентрация газа будет зависеть от температуры и давления, т.е.  . Влияние температуры передают уравнения (5) и (6). С повышением давления равновесия смещаются в сторону меньшего числа газовых молей, т.е. в случае взаимодействия (2)– вправо. Количественно влияние давления передается уравнением параболы (1). В присутствии других компонентов Me, растворенных в железе (Me–C, Si, Mn, Cr…), равновесные концентрации водорода и азота становятся иными. В частности, в трехкомпонентной системы Fe–Г2–Me равновесие двух фаз в соответствии с правилами фаз (7) характеризуется тремя степенями свободы, и
. Влияние температуры передают уравнения (5) и (6). С повышением давления равновесия смещаются в сторону меньшего числа газовых молей, т.е. в случае взаимодействия (2)– вправо. Количественно влияние давления передается уравнением параболы (1). В присутствии других компонентов Me, растворенных в железе (Me–C, Si, Mn, Cr…), равновесные концентрации водорода и азота становятся иными. В частности, в трехкомпонентной системы Fe–Г2–Me равновесие двух фаз в соответствии с правилами фаз (7) характеризуется тремя степенями свободы, и  . Это влияние в первом приближении можно учесть, используя параметры взаимодействия компонента [Me] с растворенным газом и железом. Снижение коэффициента активности и соответствующее повышение растворимости водорода вызывают: титан, ниобий, ванадий, марганец, хром, образующие с ним довольно прочные гидриды. Углерод, бор, алюминий, кремний, германий вызывают снижение растворимости водорода, а кобальт, медь, никель, молибден практически на нее не влияют. Почти в такой же последовательности влияют указанные компоненты на коэффициент активности азота и его растворимость. Сильное снижение растворимости водорода и азота при кристаллизации железа (рисунок 1) и его сплавов сопровождается рядом нежелательных явлений. Водород в молекулярном виде обособляется в дефектных местах (микропустотах) закристаллизовавшегося металла. С уменьшением размеров этих микродефектов при последующей пластической обработке он создает высокие давления, вследствие чего в металле возникают напряжения, ведущие к снижению пластичности, а иногда и к нарушению сплошности. Азот может выделяться из раствора в виде дисперсных нитридов, вызывающих сильное снижение пластичности металла и повышение его твердости. Особенности равновесия качественно справедливы и для других двухатомных газов, в частности кислорода, до таких концентраций, пока не достигнуто насыщение. Активность кислорода в железе и его сплавах обычно определяют, изучая равновесие расплава с пароводородной смесью
. Это влияние в первом приближении можно учесть, используя параметры взаимодействия компонента [Me] с растворенным газом и железом. Снижение коэффициента активности и соответствующее повышение растворимости водорода вызывают: титан, ниобий, ванадий, марганец, хром, образующие с ним довольно прочные гидриды. Углерод, бор, алюминий, кремний, германий вызывают снижение растворимости водорода, а кобальт, медь, никель, молибден практически на нее не влияют. Почти в такой же последовательности влияют указанные компоненты на коэффициент активности азота и его растворимость. Сильное снижение растворимости водорода и азота при кристаллизации железа (рисунок 1) и его сплавов сопровождается рядом нежелательных явлений. Водород в молекулярном виде обособляется в дефектных местах (микропустотах) закристаллизовавшегося металла. С уменьшением размеров этих микродефектов при последующей пластической обработке он создает высокие давления, вследствие чего в металле возникают напряжения, ведущие к снижению пластичности, а иногда и к нарушению сплошности. Азот может выделяться из раствора в виде дисперсных нитридов, вызывающих сильное снижение пластичности металла и повышение его твердости. Особенности равновесия качественно справедливы и для других двухатомных газов, в частности кислорода, до таких концентраций, пока не достигнуто насыщение. Активность кислорода в железе и его сплавах обычно определяют, изучая равновесие расплава с пароводородной смесью
 (8)
(8)
При не очень высоких давлениях константа этого равновесия
 , (9)
, (9)
а ее изменение в зависимости от температуры, по данным В.В. Аверина, определяются равенством
 (10)
(10)
Здесь активность кислорода в металле нормирована так, что  при
при  . Выражая отношение
. Выражая отношение  через
через  и константу равновесия реакции горения водорода H2+1/2O2=H2O, получаем зависимость равновесного содержания кислорода от его давления в газовой фазе
и константу равновесия реакции горения водорода H2+1/2O2=H2O, получаем зависимость равновесного содержания кислорода от его давления в газовой фазе
 (11)
(11)
При 1873 К насыщение кислородом железа с выделением FeO достигается при 0,23% [О]
В рассматриваемом равновесии паров воды с железом, как и при взаимодействии водорода с железом, содержащем кислород, в расплаве находятся кислород и водород. Влияние последнего на коэффициент активности кислорода характеризуется сравнительно высоким отрицательным значением параметра взаимодействия  , а соотношение равновесных концентраций [H] и [O] при различных парциальных давлениях паров воды определяется равенством
, а соотношение равновесных концентраций [H] и [O] при различных парциальных давлениях паров воды определяется равенством
 (12)
(12)
Константа равновесия К при 1873 равна 0,7, если давление паров воды выражено в атмосферах. При взаимодействии диоксида углерода с железом также возможно равновесие по двум независимым реакциям:
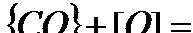 (13)
(13)
 (14)
(14)
Если реакции протекают одновременно, то система из трех компонентов (Fe, C, O) и двух фаз имеет три степени свободы: с=к+2-Ф=3+2-2=3. Следовательно, из семи переменных, определяющих ее состояние (  ), в условиях равновесия только три независимых. Если в качестве независимых принять температуру Т, давление p и состав газовой фазы, задаваемый концентрацией одного из компонентов, например
), в условиях равновесия только три независимых. Если в качестве независимых принять температуру Т, давление p и состав газовой фазы, задаваемый концентрацией одного из компонентов, например  , то для отыскания остальных величин в состоянии равновесия имеются уравнения связи:
, то для отыскания остальных величин в состоянии равновесия имеются уравнения связи:
 (15)
(15)
 (16)
(16)
Константы равновесия реакций (13) и (14):
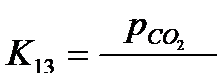 (17)
(17)
 (18)
(18)
В уравнениях (17) и (18) активности газов заменены парциальными давлениями, выраженными в атмосферах. Зависимость констант равновесия от температуры характеризуется уравнениями
 (19)
(19)
 (20)
(20)
При сравнении этих зависимостей с термодинамическим соотношением
 (21)
(21)
видно, что реакция (13) и (14) сопровождается выделением тепла, и, следовательно, с повышением температуры их равновесие смещается влево. Для реакции (14) в соответствии с равенством (20) этот эффект составляет всего -22,3 кДж/моль. Его отличие от нуля немногим превосходит погрешности измерений, поэтому равновесие (14) слабо зависит от температуры.
С повышением давления равновесие реакции (13) практически не изменяется, а равновесие реакции (14) – смещается влево. В частности, при  (0,1 МПа)
(0,1 МПа)
 (22)
(22)
Является постоянной величиной, значение которой при 1873 К равно  2*103. Произведение коэффициентов активности в пределах действия закона Генри
2*103. Произведение коэффициентов активности в пределах действия закона Генри  . Следовательно, и произведение концентраций в разбавленных растворах
. Следовательно, и произведение концентраций в разбавленных растворах
 (23)
(23)
слабо изменяется с температурой. Для анализа процессов окисления углерода, растворенного в железе, необходимо также изучение его равновесия с газовой смесью CO+CO2:
 (24)
(24)
Это взаимодействие сопровождается увеличением числа молей газа , поэтому с повышением давления равновесие смещается влево. Тепловой эффект реакции  положителен, поэтому с повышением температуры равновесное содержание CO в газовой смеси возрастает. Количественно влияние температуры на равновесие можно определить по значениям константы равновесия
положителен, поэтому с повышением температуры равновесное содержание CO в газовой смеси возрастает. Количественно влияние температуры на равновесие можно определить по значениям константы равновесия
 (25)
(25)
Поскольку система имеет три степени свободы (три компонента, две фазы), то, задавая температуру, давление и концентрацию одного из компонентов в газовой смеси, можно рассчитать равновесную активность углерода в железе.
Газы, растворяясь в железе и других металлах, диссоциируют на атомы, поэтому знак и величина теплового эффекта по закону Гесса определяется соотношением энергии конденсации газа, диссоциации соответствующих молекул и энергий растворения атомов. Сказанное относится и растворению трехатомных газов (SO2, H2S). В частности, растворимость SO2 в железе изменяется пропорционально  , что соответствует разложению молекулы на три атома – S и 2O:
, что соответствует разложению молекулы на три атома – S и 2O:
 (26)
(26)
Изменение константы равновесия с температурой
 (27)
(27)
Свидетельствует об эндотермичности процесса.
Или такой вариант…
Растворимость – макс возможная предельная конц-я при равновесии с газовой фазой
Г-растворимость, f( Г)- функц от состава
При исследовании растворимости газов оказалось, что
[%Г]~P0,5{ Г2} , эта закономерность –закон Сивертса для 3х атомного газа.
{SO2}=[O]+[S]
[% Г ]~P1/3{SO2}
Процесс растворения связан с диссоциацией молекул газа
{ Г2 }=2[ Г ]
Кр=а2 [ Г ] /p{ Г2 } =( f2 [ Г ]* [% Г ]2 )/ p{ Г2 }
[% Г ]=√( Кр* p{ Г2 }/ f2 [ Г ])
Пример: смесь кислорода и воды, смесь CO-CO2
1) { O2 }=2[ O ]
2) [O]+{ H2 }=2{H2O}
Кр=( p H2O /(f[% O ] )* p H2 )
3) {O}+2{ H2 }=2{H2O},
1)=3)-2*2)
Кр=К3 /K22
Дата добавления: 2015-04-18; просмотров: 504; Мы поможем в написании вашей работы!; Нарушение авторских прав |