Правосторонняя критическая область. Левосторонняя и двусторонняя критические области. Мощность критерия

При проверке статистических гипотез используют правосторонние, левосторонние и двусторонние критические области.

Правосторонняя критическая область характеризуется неравенством вида:

L>lкр,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр, – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия.

Следовательно, для определения правосторонней критической области необходимо рассчитать положительное значение статистического критерия l кр .

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет больше значения l кр , равна заданному уровню значимости, т.е. P(L>lкр)=a.

Для каждого статистического критерия рассчитаны специальные таблицы, с помощью которых определяют критическую точку, удовлетворяющую заданному уровню значимости.

Левосторонняя критическая область характеризуется неравенством вида:

L<lкр,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр, — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия.

Следовательно, для определения левосторонней критической области необходимо найти рассчитать отрицательное значение статистического критерия l кр .

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, вероятность того, что значение статистического критерия L будет меньше значения l кр , равна заданному уровню значимости, т.е. P(L<lкр)=a.

Двусторонняя критическая область характеризуется двумя неравенствами вида:

L>lкр1 и L<lкр2,

где L – это наблюдаемое значение статистического критерия, вычисленное по данным выборки;

lкр1 – это положительное значение статистического критерия, определяемое по таблице распределения данного критерия;

lкр2 — это отрицательное значение статистического критерия, определяемое по таблице распределения данного критерия;

lкр1> lкр2.

Предположим, что вероятность совершения ошибки первого рода или уровень значимости равен значению а. При условии справедливости основной гипотезы Н0, сумма вероятностей того, что значение статистического критерия L будет больше значения l кр1 или меньше значения l кр2 , равна заданному уровню значимости, т.е. P(L>lкр1)+(L<lкр2)=a.

Выбор критической области осуществляется исходя из вида конкурирующей гипотезы Н1. При этом применяются следующие правила:

1) правосторонняя критическая область выбирается в том случае, если Н1:>;

2) левосторонняя критическая область выбирается в том случае, если Н1:‹;

3) двусторонняя критическая область выбирается в том случае, если Н1:≠.

Предположим, что заданы следующие параметры:

1) статистический критерий L;

2) критическая область W, где H0 отклоняется;

3) область принятия гипотезы

где H0 не отклоняется;

4) вероятность совершить ошибку первого рода a;

5) вероятность совершить ошибку второго рода β.

Тогда справедливо утверждение о том, что выражение

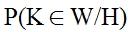
является вероятностью того, что статистический критерий L попадёт в критическую область, если верна гипотеза H.

При построении критической области учитываются два требования:

1) вероятность того, что статистический критерий L попадёт в критическую область, если верна Н0, равна а:

данное равенство задаёт вероятность совершения ошибки первого рода;

2) вероятность того, что статистический критерий L попадёт в критическую область (область отклонения гипотезы Н0 в пользу гипотезы Н1), если верна гипотеза Н1:

данное равенство задаёт вероятность принятия правильной гипотезы.

Мощностью статистического критерия называется вероятность попадания данного критерия в критическую область, при условии, что справедлива конкурирующая гипотеза Н1, т. е.выражение 1-β является мощностью критерия.

Если уровень значимости уже выбран, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования обеспечивает минимальную ошибку второго рода, состоящую в том, что будет принята неправильная гипотеза.