
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Проверка гипотезы о значимости коэффициентов модели парной регрессии
Проверкой статистической гипотезы о значимости отдельных параметров модели называется проверка предположения о том, что данные параметры значимо отличаются от нуля.
Необходимость проверки гипотез о значимости параметров модели вызвана тем, что в дальнейшем построенную модель будут использовать для дальнейших экономических расчётов.
Предположим, что по данным выборочной совокупности была построена линейная модель парной регрессии. Задача состоит в проверке значимости оценок неизвестных коэффициентов модели, полученных методом наименьших квадратов.
Основная гипотеза состоит в предположении о незначимости коэффициентов регрессии, т. е.
Н0:β0=0, или Н0:β1=0.
Обратная или конкурирующая гипотеза состоит в предположении о значимости коэффициентов регрессии, т.е.
Н1:β0≠0, или Н1:β1≠0.
Данные гипотезы проверяются с помощью t-критерия Стьюдента.
Наблюдаемое значение t-критерия (вычисленное на основе выборочных данных) сравнивают со значением t-критерия, которое определяется по таблице распределения Стьюдента и называется критическим.
Критическое значение t-критерия зависит от уровня значимости и числа степеней свободы.
Уровнем значимости а называется величина, которая рассчитывается по формуле:
а=1-γ,
где γ – это доверительная вероятность попадания оцениваемого параметра в доверительный интервал. Значение доверительной вероятности должно быть близким к единице, например, 0.95, 0.99. Следовательно, уровень значимости а можно определить как вероятность того, что оцениваемый параметр не попадёт в доверительный интервал.
Числом степеней свободы называется показатель, который рассчитывается как разность между объёмом выборочной совокупности n и числом оцениваемых параметров по данной выборке h. Для линейной модели парной регрессии число степеней свободы рассчитывается как (n-2 ), потому что по данным выборочной совокупности оцениваются только два параметра – β0 и β1 .
Таким образом, критическое значение t-критерия Стьюдента определяется как tкрит(а;n-h).
При проверке основной гипотезы вида Н0:β1=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:


где – оценка параметра модели регрессии β1 ;
ω(β1 ) – величина стандартной ошибки параметра модели регрессии β1 .
Показатель стандартной ошибки параметра модели регрессии β1 для линейной модели парной регрессии рассчитывается по формуле:

Числитель стандартной ошибки может быть рассчитан через парный коэффициент детерминации следующим образом:
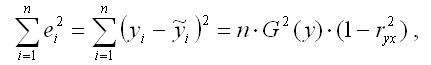
где G2(y) – общая дисперсия зависимой переменной;
r2yx – парный коэффициент детерминации между зависимой и независимой переменными.
При проверке основной гипотезы β0=0 наблюдаемое значение t-критерия Стьюдента рассчитывается по формуле:

где
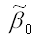
– оценка параметра модели регрессии β0;
ω(β0) – величина стандартной ошибки параметра модели регрессии β0.
Показатель стандартной ошибки параметра β0 модели регрессии для линейной модели парной регрессии рассчитывается по формуле:

При проверке основных гипотез возможны следующие ситуации:
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю больше критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|›tкрит, то с вероятностью (1-а) или γ основная гипотеза о незначимости параметров модели регрессии отвергается.
Если наблюдаемое значение t-критерия (вычисленное по выборочным данным) по модулю меньше или равно критического значения t-критерия (определённого по таблице распределения Стьюдента), т. е. |tнабл|≤tкрит, то с вероятностью а или (1-γ) основная гипотеза о незначимости параметров модели регрессии принимается.
Дата добавления: 2015-04-18; просмотров: 244; Мы поможем в написании вашей работы!; Нарушение авторских прав |