Методы Кохрана-Оркутта и Хилдрета-Лу оценки коэффициента автокорреляции

Помимо вычисления выборочного коэффициента автокорреляции остатков оценку автокорреляционного коэффициента β можно рассчитать методом Кохрана-Оркутта.

Предположим, что на основе собранных наблюдений была построена линейная парная модель регрессии:

yt=β0+β1xt+εt.(1)

Рассмотрим применение метода Кохрана-Оркутта оценки коэффициента автокорреляции на примере данной модели.

Осуществление метода Кохрана-Оркутта происходит в несколько этапов.

1) оценки неизвестных коэффициентов исходной модели регрессии определяются классическим методом наименьших квадратов. В результате мы получим оценённую модель регрессии вида:

2) на основании исходной (1) и оценённой (2) моделей регрессии рассчитываются остатки модели:

3) рассчитывается выборочный автокорреляционный коэффициент первого порядка по формуле:

С помощью данного коэффициента можно оценить авторегрессионную зависимость остатков:

4) строится преобразованная модель регрессии. Модель регрессии в момент времени (t-1 ) может быть представлена виде yt-1=β0+β1xt-1+εt-1.(3) . Если модель регрессии в момент времени (t-1 ) умножить на величину коэффициента автокорреляции β и вычесть её из исходной модели регрессии в момент времени t , то в результате мы получим преобразованную модель регрессии, учитывающую процесс автокорреляции первого порядка:

Для более наглядного представления преобразованной модели воспользуемся методом замен:

Yt=yt–ρyt-1;

Xt=xt–ρxt-1;

Zt=1– ρ .

В результате преобразованная модель регрессии примет вид:

Yt= Zt* β0+β1 Xt+ νt. (5)

5) оценки неизвестных коэффициентов преобразованной модели регрессии рассчитываются с помощью традиционного метода наименьших квадратов:

Далее рассчитываются оценки коэффициентов исходной модели регрессии по формулам:

В результате полученную модель регрессии можно представить в виде:

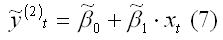
6) на заключительном этапе вновь вычисляются остатки et между исходной (1) и преобразованной оценённой (7) моделями регрессии, и процесс повторяется с третьего этапа.

Метод Кохрана-Оркутта является итеративным методом оценивания. Его основное отличие состоит в том, что процесс итеративного оценивания исходной модели регрессии сходится или останавливается при условии, если последнее вычисленное значение оценки коэффициента автокорреляции первого порядка ρ1 почти не отличается от своего предыдущего значения.

Другим методом вычисления оценки коэффициента автокорреляции является метод Хилдрета-Лу.

В этом случае коэффициент автокорреляции задаётся двумя параметрами: диапазоном и величиной шага. Например, коэффициента автокорреляции ρ 1 заключается в пределах [-1;+1 ], и его значения вычисляются с шагом 0,02.

Для каждого из значений коэффициента автокорреляции с помощью метода разностей строится преобразованная модель регрессии вида:

Yt= Zt* β0+β1Xt+ νt,

где Yt=yt–ryt-1;

Xt=xt–rxt-1;

Zt=1–r .

Далее оценки неизвестных коэффициентов преобразованной модели регрессии рассчитываются с помощью классического метода наименьших квадратов:

Оценкой коэффициента автокорреляции первого порядка ρ1 будет являться то значение коэффициента, с помощью которого вычисляется минимальная сумма квадратов отклонений теоретических значений от расчётных значений (на основе преобразованной модели регрессии).

Оценки неизвестных коэффициентов результативной модели регрессии рассчитываются по формулам:

65. Обобщённая модель регрессии. Обобщённый метод наименьших квадратов. Теорема Айткена

МНК-оценки неизвестных коэффициентов модели регрессии, чьи случайные ошибки подвержены явлениям гетероскедастичности или автокорреляции, не будут удовлетворять теореме Гаусса-Маркова. Свойствами состоятельности и несмещённости МНК-оценки будут обладать, однако свойство эффективности в этом случае утрачивается.

Для вычисления оценок неизвестных коэффициентов модели регрессии с гетероскедастичными или коррелированными случайными ошибками используется обобщённый метод наименьших квадратов. Оценки, полученные с помощью данного метода, будут удовлетворять условиям состоятельности, несмещённости и эффективности.

В основе нормальной линейной модели регрессии среди прочих лежат условия о некоррелированности и гомоскедастичности случайных ошибок:

1) дисперсия случайной ошибки модели регрессии является величиной, постоянной для всех наблюдений:

2) случайные ошибки модели регрессии не коррелированны между собой, т. е. ковариация случайных ошибок любых двух разных наблюдений равна нулю:

Определение. Обобщённой линейной моделью регрессии называется модель, для которой нарушаются условия о гомоскедастичности и некоррелированности случайных ошибок.

Таким образом, обобщённая линейная модель регрессии характеризуется неоднородностью дисперсий случайных ошибок:

D(εi)≠ D(εj)≠G2≠const, где i≠j,

и наличием автокорреляции случайных ошибок:

Cov(εi,εj)≠E(εi,εj)≠0 (i≠j).

Матричный вид обобщённой линейной модели регрессии:

Y=X* β+ε,

где X – неслучайная матрица факторных переменных;

ε – случайная ошибка модели регрессии с нулевым математическим ожиданием E(ε)=0 и дисперсией G2(ε):

ε~N(0;G2Ω),

Ω – ковариационная матрица случайных ошибок обобщённой модели регрессии.

Для нормальной линейной модели регрессии дисперсия случайной ошибки определялась на основе условия гомоскедастичности:

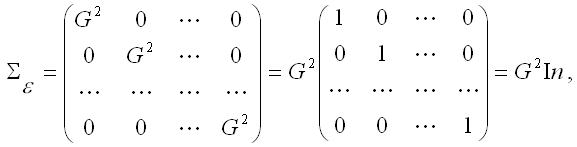
где G2=const – дисперсия случайной ошибки модели регрессии ε ;

In – единичная матрица размерности n*n .

Для обобщённой модели регрессии ковариационная матрица случайных ошибок строится на основе условия непостоянства дисперсий остатков модели регрессии (гетероскедастичности) D(εi)≠ D(εj)≠G2≠const :

Отличие между нормальной линейной моделью регрессии и обобщенной линейной моделью регрессии заключается в матрице ковариаций случайных ошибок модели.

Теорема Айткена . В классе линейных несмещённых оценок неизвестных коэффициентов обобщённой модели регрессии оценка

будет иметь наименьшую ковариационную матрицу.

Общая формула для расчёта матрицы ковариаций ОМНК-оценок коэффициентов обобщенной модели регрессии имеет вид:

Величина G2(ε) оценивается по формуле:

Однако значение G2(ε) не следует трактовать как дисперсию случайной ошибки модели регрессии.

Коэффициент детерминации не используется при оценке качества обобщённой линейной модели регрессии, потому что он не отвечает требованиям, предъявляемым к обычному множественному коэффициенту детерминации.

Проверка гипотез о значимости коэффициентов обобщенной линейной модели регрессии и модели регрессии в целом осуществляется с помощью тех же статистических критериев, что и в случае нормальной линейной модели регрессии.

66. Доступный обобщённый метод наименьших квадратов. Взвешенный метод наименьших квадратов

Если случайные ошибки модели регрессии подвержены процессу автокорреляции, то для оценивания неизвестных коэффициентов модели регрессии применяется доступный обобщённый метод наименьших квадратов.

Основное отличие доступного обобщённого метода наименьших квадратов от обобщённого метода заключается в оценке матрицы ковариаций β случайных ошибок обобщенной линейной модели регрессии.

Оценки неизвестных коэффициентов обобщённой модели регрессии рассчитываются с помощью доступного обобщённого метода наименьших квадратов по формуле:

где

– оценка матрицы ковариаций случайных ошибок обобщённой линейной модели регрессии.

Предположим, что на основе собранных данных была построена модель парной регрессии вида:

yt=β0+β1xt+εt.(1)

Рассмотрим процесс оценивания матрицы ковариаций случайных ошибок модели с автокоррелированными, но гомоскедастичными остатками на примере данной модели.

Если остатки данной модели регрессии подчиняются авторегрессионному процессу первого порядка, то исходную модель регрессии можно представить в виде:

yt=β0+β1xt+ ρεt-1+νt,.

εt=ρεt-1+νt,

где ρ – коэффициент автокорреляции, |ρ|< 1;

νt – независимые, одинаково распределённые случайные величины с нулевым математическим ожиданием и дисперсией G2(νt).

Математическое ожидание случайной ошибки модели регрессии равно нулю:

E(εt)=E(ρεt-1+νt)= ρE(εt-1)+E(νt)=0.

Предположим, что дисперсия случайной ошибки модели регрессии рассчитывается по формуле:

Рассчитаем ковариацию между двумя соседними случайными ошибками модели регрессии ε2 и ε1 :

Рассчитаем ковариацию между следующими случайными ошибками модели регрессии ε3 и ε1:

Дальнейший процесс расчёта ковариаций для всех случайных ошибок обобщенной модели регрессии осуществляется по тому же принципу.

В результате проведённых вычислений матрицу корреляций остатков обобщённой линейной модели регрессии можно представить следующим образом:

где G2(νi) – это величина дисперсии случайной ошибки модели регрессии. Её выборочную оценку определяется по формуле:

где T – объём выборочной совокупности;

h – число оцениваемых по выборке параметров.

Если случайные ошибки модели регрессии подвержены гетероскедастичности (но являются неавтокоррелированными), то для оценивания неизвестных коэффициентов модели регрессии применяется взвешенный метод наименьших квадратов.

Суть взвешенного метода наименьших квадратов состоит в том, что остаткам обобщённой модели регрессии придаются определённые веса, которые равны обратным величинам соответствующих дисперсий G2(εi). Однако на практике значения дисперсий являются величинами неизвестными, поэтому для вычисления наиболее подходящих весов используется предположение о том, что они пропорциональны значениям факторных переменных xt .

Таким образом, матрица ковариаций случайных ошибок модели регрессии определяется исходя из предположения о пропорциональности величины G2(εi) значениям факторной переменной xt :

xt=γ G(εi),

где γ – ошибка высказанного предположения или некоторая поправка.

В этом случае матрица ковариаций случайных ошибок модели регрессии может быть представлена в виде:

От точности оценки матрицы ковариаций Ω случайных ошибок модели регрессии зависит удовлетворение оценок неизвестных коэффициентов, полученных доступным обобщённым или взвешенным методом наименьших квадратов, основным статистическим свойствам – несмещённости, состоятельности и эффективности.