
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Устранение автокорреляции остатков модели регрессии
В связи с тем, что наличие в модели регрессии автокорреляции между остатками модели может привести к негативным результатам всего процесса оценивания неизвестных коэффициентов модели, автокорреляция остатков должна быть устранена.
Устранить автокорреляцию остатков модели регрессии можно с помощью включения в модель автокорреляционного параметра, однако на практике данный подход реализовать весьма затруднительно, потому что оценка коэффициента автокорреляции является величиной заранее неизвестной.
Авторегрессионной схемой первого порядка называется метод устранения автокорреляции первого порядка между соседними членами остаточного ряда в линейных моделях регрессии либо моделях регрессии, которые можно привести к линейному виду.
На практике применение авторегрессионной схемы первого порядка требует априорного знания величины коэффициента автокорреляции. Однако в связи с тем, что величина данного коэффициента заранее неизвестна, в качестве его оценки рассчитывается выборочный коэффициент остатков первого порядка ρ1 .
Выборочный коэффициент остатков первого порядка ρ1 рассчитывается по формуле:
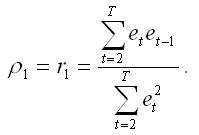
В общем случае коэффициент автокорреляции порядка l рассчитывается по формуле:

где l – временной лаг;
T – число наблюдений;
t – момент времени, в который осуществлялось наблюдение;

– среднее значение исходного временного ряда.
Предположим, что на основе собранных наблюдений была построена линейная парная модель регрессии:
yt=β0+β1xt+εt.(1)
Рассмотрим применение авторегрессионной схемы первого порядка на примере данной модели.
Исходная линейная модель парной регрессии с учётом процесса автокорреляции остатков первого порядка в момент времени t может быть представлена в виде:
yt=β0+β1xt+ ρεt-1+νt,.
εt=ρεt-1+νt,
где ρ – коэффициент автокорреляции, |ρ|<1 ;
νt – независимые, одинаково распределённые случайные величины с нулевым математическим ожиданием и дисперсией G2(νt).
Модель регрессии в момент времени (t-1 ) может быть представлена виде:
yt-1=β0+β1xt-1+εt-1.(2)
Если модель регрессии в момент времени (t-1 ) умножить на величину коэффициента автокорреляции β и вычесть её из исходной модели регрессии в момент времени t , то в результате мы получим преобразованную модель регрессии, учитывающую процесс автокорреляции первого порядка:

Для более наглядного представления преобразованной модели воспользуемся методом замен:
Yt=yt–ρyt-1;
Xt=xt–ρxt-1;
Zt=1– ρ .
В результате преобразованная модель регрессии примет вид:
Yt= Zt* β0+β1 Xt+ νt. (4)
В преобразованной модели регрессии случайная ошибка βt не подвержена процессу автокорреляции, поэтому можно считать автокорреляционную зависимость остатков модели устранённой.
Авторегрессионную схему первого порядка можно применить ко всем строкам матрицы данных Х , кроме первого наблюдения. Однако если не вычислять Y1 и X1 , то подобная потеря в небольшой выборке может привести к неэффективности оценок коэффициентов преобразованной модели регрессии. Данная проблема решается с помощью поправки Прайса-Уинстена. Введём следующие обозначения:

Тогда оценки неизвестных коэффициентов преобразованной модели регрессии (4) можно рассчитать с помощью классического метода наименьших квадратов:

Оценки коэффициентов исходной модели регрессии (1) определяются по формулам:

В результате оцененная модель регрессии будет иметь вид:

Дата добавления: 2015-04-18; просмотров: 331; Мы поможем в написании вашей работы!; Нарушение авторских прав |