
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ц111Г1Г11,ЦТ>Г11>Г/'>ГЧ"1ТГ 1 страница
, а
Тогда в безнапорном и напорном потоках уровень жидкооти в трубке поднимется на выше уровня свободной поверхнооти
безнапорного потока или выше уровня жидкости в пьезометре напорного потока, так как движущаяся жидкость будет оказывать дополнительное давление, близкое к давлению столба жидкости высотой иг/2$- . Такая трубка называется по имени ученого трубкой Пито, предложившего ее в 1732 г. для измерения окорооти движущейся жидкости.
Полная удельная энергия е.по*н складывается из удельной потенциальной и кинетической энергии: е„олн = впот * екиМ = г +• р/р% -»- (3.15)
В технической литературе вместо термина "удельная энергия" употребляют термин "напор", вместо удельной потенциальной энергии - пьезометрический напор (потому что он измеряется пьезо-' метрами), вместо удельной кинетической энергии - скороотной напор, вместо полной удельной энергии - полный, или гидродинамический, напор. 7
З.4. Уравнение Д.Бернулли
Рассмотрим движение жидкости от живого сечения I к живому оечению 2 (рис. 3.9). а
| 3 — _ — _ | |
т " •■
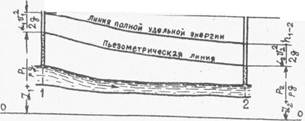 Рис. 3.9. К уравнению Д.Бернулли.
Рис. 3.9. К уравнению Д.Бернулли.
|
Движение жидкости в сечениях I и 2 плавноизменяющееоя. Оп- ределим полную удельную энергию в сечении I.
Для этого к удельной потенциальной энергии ечот.) + нужно прибавить удельную кинетическую энергию. Обозначим среднюю окорооть в первом сечении IГ, . Если бы во всех точках сечения I скорости были одинаковы и равнялись \Г, , то еким.1 = . Но скорости по оечению I различны, поэтому удельная кинетическая энергия в нем может быть выражена чер^з среднюю скорость 1Г, только при условии введения поправочного коэффициента об , называемого в гидравлике коэффициентом Кориолиса.
Следовательно, Еким.» = <6,, а 1 + р^+^у^/г^ . Аналогично определяется полная удельная энергия в сечении
2: - Яа. + Рг/р^^^/г^.
Поскольку на пути от сечения 1 до сечения 2 часть механической энергии расходуется на преодоление сопротивлений движению, 1 > 2 . Израсходованную часть удельной энергии ■жидкости называют потерей напора и обозначают обычно Ь,.а . На основании закона о сохранении энергии можно
написать
а так как , то
" + Г + + + ■ (3.16)
Это уравнение называют уравнением Д.Б е р - н у л л и; Все члены этого уравнения имеют линейную размерность. Откладывая вверх от плоскости сравнения 0-0 для всех живых сечений гидростатический бином (пьезометрический налор) 3.4'р/^- , получаем линию, которая называется пьезометрической. 'Откладывая вверх от пьезометрической линии для всех живых сечений значения удельной кинетической энергии оСгг^/г^. . получаем линию полной удельной
энергии.
Линия полной удельной энергии может только опускаться,
так как удельная энергия в направлении движения уменьшается. Пьезометрическая линия в зависимости от скорости может снижаться вдоль течения (пр5, увеличении окорооти), идти вверх (при уменьшении скорости) и быть горизонтальной.
Проведя горизонтальную прямую тп на расотоянии '
от плоскооти оравнения 0-0 , получим для сечения 2 между ли
нией тп и линией полной энергии вертикальный отрезок, который представляет собой потерю напора Ь,-2 на пути от сечения I до сечения 2.
Понижение линии полной удельной энергии (или изменение удельной энергии) на единицу длины потока называется гидравлическим уклоном и обозначается I . Гидравлический уклон при длине потока Ь
1 = Ь,_2/Ь, (3.17)
а пьезометрический
1п = 1/1 (3.18) Для безнапорных потоков, находящихся под атмосферным давлением, их свободная поверхность и пьезометрическая линия совпадают, а уклон свободной поверхности таких потоков - это пьезометрический уклон.
В уравнении 3.16 коэффициент Кориолиса X (коэффициент кинетической энергии) представляет собой корректив при исчислении удельной кинетической энергии по средней скорости гГ . -Его величина зависит от формы эпюры местных скоростей в живом сечении, и соответственно от.степени ее отклонения от равномерного распределения. Если распределение скоростей равномерное, то для всех элементарных струек ы = гГ и коэффициент оС= 1. Если эпюра местных окоростей значительно отличается от равномерной, ТО о6»>
В отдельных случаях, в том числе при турбулентном движении жидкооти через дорожные водопропускные и водобойные сооружения, локальные значения коэффициента Кориолиса могут достигать нескольких единиц. Расчеты по средней скорости приведут к заниженному в несколько раз значений кинетической энергии потока, его динамического .воздействия на сооружение и русло, что может иметь катастрофические последствия.
По данным В.Н.Евреинова (цит. по ^приближенно можно очитать , ,„г
~ 1+210/Ъ , (319)
где С- коэффициент Шези в формуле определения средней ско- рооти потока по гидравличеокому радиусу и уклону. —
А.Д.Альтшуль предложил определять коэффициент оС по формуле
+ (э<20)
где \ - коэффициент сопротивления по длине.
Более точное определение коэффициента Кориолиса приводит-
С- 43 -
с я в работе С2Я •
При менее точных расчетах принимают Х= I, и тогда уравнение Д.Бернулли (3.16) имеет следующий вид:
д, г р«/г * КАэ +' - (3,21)
3.5. Потери напора Потери напора на преодоление гидравлических сопротивлений включают: I) потери напора по длине потока (линейные) и
*) местное потери напора Ь„, обусловленные резкоизменяющимся 41ижениеч (вход в трубу, повороты, расширения, вентили, задвижки и т.п.). То есть полные потери напора на участке 1-2 равны сумме потерь:
Потери энергии по длине и местные потери имеют одну и ту же физическую природу: это результат преобразования части механической энергии в тепловую за счет преодоления касательных напряжений трения. Разница между ними состоит в том, что путевые потери нарастают по длине постепенно, обеопечивая постоянный гидравлический уклон, то есть постоянную интенсивность потерь, а местные потери энергии связаны с локальной концентрацией касательных усилий в зоне действия меотного сопротивления.
Потери напора по длине в трубопроводах обычно определяют по формуле Дарси-Вейсбаха:
"" (3.22)
а в открытых руслах - по формуле Шези:
К'Л/С^. 0.23)
Здеоь X -...коэффициент.трения (коэффициент Дарси) ; 1,а, * И й - соответственно длина участка трубы или канала, диаметр трубы, средняя скорость течения и гидравлический радиус; для круглых труб В- с//4 , или о[* 4К ; С- коэффициент Шези.
Величина коэффициентов А и С обусловливается особенностями движения жидкости. Связь между ними имеет вид
Х=8Э/С2 ; С'^/Г , млУ« (вг системе СИ). (3.24) Формулы для определения коэффициента трения (Я) приведены в работе [гу\ . При приближенных расчетах рекомендуется принимать следующие его значения: для чугунных и сварных стальных труб 0,02; для бетонных и железобетонных 0,022 и деревянных
0,019 [201-
Местные потери напора определяют по формуле Вейсбаха:
Ь„(Э«25)
где 6 - коэффициент местного сопротивления; тГ - средняя ско- рооть в сечении, расположенном ниже по течению за данным сопротивлением.
Значения коэффициента местного сопротивления ( 4 ) берутся из таблиц, приводимых в справочниках по гидравлике ГЗД. Значения его для нек торых видов местных сопротивлений: вход в трубу при острых кромках - 0,50; плавный вход в трубу - 0,05*0,20; резкий поворот трубы на 90° - 1,20; плавный поворот на 90° - 0,15; различные вентили при полном открытии - 2,5-6.0; задвижка при полном открытии - 0,11*0,12; то же на 3/4 - 0,26; то же на 1/2 - 2,0 и на 1/4 - П.
При наличии в системе нескольких местных сопротивлений для определения меотных потерь напора по формуле (3.25) коэффициенты меотных сопротивлений складываются^.
3.6. Формула Шези
В ряде олучаев, особенно при расчетах безнапорных потоков, возникает необходимость определять скорооть движения и другие характеристики по известным потерям энергии, а точнее - по заданному гидравлическому уклону ь-=ксЛ.
В качестве иоходной можно использовать формулу (3.22) Дарои-Вейсбаха, решая при этом обратную задачу. Подставляя в • нее известные выражения 1-^/1 , и (3.24), получаем
так называемую формулу Шези:
иГ^^УйГ „СШ. , (3.26) *
/Г-С/7Г (3.27)
- окоростная характеристика (модуль скорости), она численно равна, скорости при гидравлическом уклоне, равном единице. Известно, что размерность окорост- ной характеристики совпадает о размерноотью скорости.
На базе формулы Шези (3.26) можно записать выражение расхода
>■ О-сйСШ =Х/Г, (3,28)
где
(3>29)
- расходная характеристика (модуль раохода), величина, численно равная расходу при гидравлическом уклоне, равном единице. Размерности расхода и расходной характеристики тоже одинаковы.
Полученные выше формулы, как уже отмечалось, широко применяются при описании движения безнапорных потоков. Но они используются и в расчетах напорных систем при равномерном движении, например трубопроводов. Потери напора при этом, учитывая I «= , равны:
Ь.-Л/Ь'Я-Л/Г*; ЧУС2К =вЧ/Х2. (з.зо)
3.7. Истечение жидкости из отверотий и насадков
Отверстия и насадки широко применяются в технике (жиклеры и форсунки двигателей, наконечники гидромониторов и брандспойтов и т.д.). В гидротехническом строительстве иотечение жидкости из отверстий и насадков используется в гидравлических расчетах сифонов, дюкеров, дорожных труб, донных водоспусков в плотинах и других гидротехнических сооружений.
Напорные оистемы, в которых местные потери энергии и поте ри на трение по длине соизмеримы (^„««з^ ), отнооят к коротким трубам.
Типичный олучай коротких труб - напорные водопропускные трубы, уложенные под наоыпью дорог и в плотинах. В методике их раочета иопользуютоя сведения и о работе насадков. В то же вре мя короткие трубы могут работать й по принципу истечения через
отверстия в тонкой стенке.
Короткие патрубки, в которых местные потери значительно превосходят потери по длине ^хЬ^ ), относят к насад
кам.
В гидравлике отверстия для истечения жидкости разделяют на малые и большие. Малыми называют такие, поперечный размер которых не превышает 0,1Н (напора)'. Важное значение при истечении жидкости через отверстия имеет толщина стенок. Различают отверотия в тонкой (рис. 3.10, а) и толотой (б) стенках.


Рис. ЗЛО. Истечение жидкости из отверотия в тонкой (а) и толотой (б) стенках.
_ Отверстие в тонкой стенке не влияет на форму отруи, у него толщина стенки I меньше трех диаметров ( ), где сI -
диаметр отверстия.
При отверстия считаются в толстой стенке. К ним
относят и короткие патрубки, прикрепленные к отверстиям в ..он
кой стенке и называемые насадками. Насадки бывают (рис. 3.11) цилиндрические (внешние - а и внутренние - б), конические с различным углом конусности (сходящиеся - в и расходящиеся - г) и коноидальные (по форме струи - д).

|
| г |
Р<31 С х о"^

|
Р^МлД, 4 'в г
Рис. 3.11, Типы насадков.
Из отверстий жидкость может вытекать или непосредственно в атмосферу (незатопленные отверстия), или под уровень в другой сосуд (затопленные отверотия). В первом случае жидкость находится под напором (Н ), равным расстоянию от поверхности до центра тяжести отверстия, а во втором г напор равен разности уровней жидкости в двух сосудах (.Л-Н,-Н2 ).
При истечении жидкости через отверстие происходит сжатие отруи (ом. рис. 3.10), которое учитывается коэффициентом сжатия (б). При этом а)с=е«*> где - площадь сжатого сечения отруи; и) - площадь сечения отверстия. Для большинства случаев истечения воды из круглых и других форм отверстий при <1 > 1 ом приближенно можно принимать: 6 « 0,61+0,63. Определение е приводится в работе [%}] ,
Скорость истечения отруи из отверстия ( ) при постоянном напоре и без учета окорооти подхода («Гв ) может быть определена по формуле .
где <? - коэффициент окорооти, выр&жающий отношение действительной скорооти к скорости истечения идеальной жидкости; приближенно можно принимать Vе 0,97+0,98.
Основная формула определения раохода жидкости из отверо- тий и наоадков при постоянном напоре и без учета скорооти подхода имеет вид ,—
5=«ги)с — еуДуЗдН ^рДуЦ", (3.32)
где еч-/! - коэффициент расхода, учитывающий одновременно коэффициенты сжатия и скорости. Значение коэффициента раохода С^» для малого отверотия в тонкой стенке - 0,62; для большого отверстия - 0,70; для ^щсадков: внешнего цилиндрического с острой входной кромкой к-^зТб^а при входной^кромке скругленной - 0,95; внутреннего цилиндрического - 0,71; конически схо- дящегос ( в среднем при угле конуснооти от 12 до 15°) - 0,94; конически расходящегося - 0,45*0,50; коноидального - 0,98.
В практике иногда приходится решать обратную задачу: по известному расходу подбирать диаметр отверстия насадка. В этом случае в формулу (3.32) подставляют <й=лг с//4 и получают А . (3.33)
Длина коротких патрубков, которая обеспечивает их работу как цилиндрических насадков, то есть практически без влияния сопротивлений по длине, составляет 3,5 <А < Ь < (6*7)сА . При 1-е 3,5сА образуется зазор между струей и внутренней поверхностью патрубка, воздух поступает в зону сжатия струи, что исключает образование вакуума.-В зоне сжатия давление будет равно атмосферному и патрубок будет работать как отверстие в тонкой отенке о коэффициентом расхода п 0,62.
Существует ограничение нормальной устойчивой работы насадков по напору, который должен быть в пределах Нв<Н<Нпр. При Н *0,5с1 на поверхности питающего резервуара возникает воронка, по которой воздух засасывается в насадок с верхней стороны. При таком условии вакуум не возникает и насадок работает как отверстие в тонкой стейке, а коэффициент расхода (у* ) равен 0,62. При напорах выше предельного №>Н ) струя отрывается от стенок насадка. Воздух засасывается в зону сжатия струи,и вакуум иочезает. Поэтому предельный напор для цилиндрического насадка ооотавляет около 13,8 м. Обычно его принимают с некоторым запа-
оом (Ю + 12 м).
Пример 3.6. Определить расход и скорость истечения
воды в атмосферу через отверстие в тонкой стенке, если напор ■ над центром тяжести отверстия Н = 2,5 м, а площадь отверстия - 8 см2.
Решение. Используем формулу (3.32). Поскольку диаметр отверстия меньше 0,Ш, оно относится к малым и коэффициент расхода ^ « 0,62. Необходимо помнить, что величины, ио- ипльэуемые при определении, должны быть в одноименных единицах иемпрения. С учетом этого » 8 см /10000 * 8-1СГ м .
"0,62-8-10" /2^9,81 • 2,5 - 0,00347 м7о -
1,47 я/о.
Для определения скорости используем формулу (3.31). ^т^ЩЖ- 0,98 {2^9,81-2,^' 6,9 м/с.
Пример 3.7. Определить диаметр водоспуска, спроекти- р»намного в теле плотины в виде трубы длиной I « 5 м. Напор над
водоспуском при свободном истечении Н -6,5 м, а расход воды О' 12 м3/о.
Решение. Используем формулу (3.33). Принимаем, что водоопуок работает ка1&'цилиндрический внешний насадок, то есть
* 0,82. Определяем диаметр водоспуска: аI «/40' - ^4-12/3,14-0,82 V2-9,81-6,5" - 1,3 м. Поокольку 1/1 = 5/1,3 - 3,9, водоспуск будет работать как насадок с коэффициентом расхода 0,82.
Еоли это соотношение меньше 3,5, то диаметр водоспуска нужно^было бы определить о использованием коэффициентов расхода: 0,62 (малое отверстие) или 0,70 (большое). При соотношении 1/<1>Ч систему необходимо рассматривать как трубопровод.
Пример 3.8, Определить расход и скорость истечения воды через трубу в плотине, если напор над центром трубы Н = ' 6 м, с1 « 3 м, длина трубы Юн.
Решение. Для определения расхода по формуле (3.32) необходимо установить, к какой напорной системе относится данное сооружение. Соотношение 1/<1<Э,5 и, кроме того, <^>0,1Н. Следовательно, принимаем коэффициент расхода С,70 (большое отверстие).
0,70(3,14.32/4)\/2-9,81-б'- 53,7 м3/с. Скорость определяем по формуле (3.31)
Ъ^уЩЯш 0,98У2- 9,81- 6 = 10,6 м/с.
Пример 3.9. Определить расход воды, проходящей че-> рез цилиндрический насадок длиной 11« 100 мм и диаметром с1 - 100 мм под напором Н ■= 4 м. Сравнить с работой насадка при * 400 мм.
Решение. I. Выясним уоловия работы цилиндрического насадка. Заданный напор Н * 4 м меньше предельного для цилиндрических насадков напора НПр - 10 м, то есть при таком напоре насадок может работать полной площадью выходного сечения. Но отношение длины к диаметру = 100/100 « 1 меньше допускаемого отношения (6 + 7)>Ь/А > 3,5. При длине 100 мм сжатая на входе насадка струя не успеет расшириться на выходе до стенок насадка. Поэтому в зоне сжатия давление равно атмосферному, и насадок будет работать как отверстие в тонкой стенке с коэффициентом расхода Ц * 0,62. Определим расход При этих условиях; !_,
„ 0,62((3,14 (0,1)2/4))/?9Г81:Т- 0,0431м3/с.
2. При длине насадка - 400 мм соблюдаются оба условия, необходимые для его нормальной работу (напор и относительная длина). В этом случае коэффициент расхода насадка = 0,82. Находим расход
а= 0,82 ((3,14 (О.^Л^Уг7^?^ 0,057 м3/о.
2 2 3.8. Гидравличеокий расчет трубопроводов Трубопроводом называется сооружение, состоящее из соединенных между собою труб и служащее у\ля транспортировки воды (нефти, газа и пр.) из мест добычи в районы потребления и переработки. У трубопроводов, относящихся к напорным системам в общей сумме местные потери энергии пренебрежимо малы (5/)„ 5 ) и могут учитываться суммарно (5-15$ от потерь по длине).
Примером трубопроводов могут быть водопроводные линии, * имеющие при значительной протяженности относительно малое количество регулирующих, запорных и других уотройств. На городских линиях длиной свыше 200 м при диаметре до 200-500 мм местные потери энергии не превышают 3-5% от потерь подлине. В то же время линии такой же длины, предназначенные для подачи сырья и продукции, например на нефтехимических заводах, как правило, насыщены местными сопротивлениями значительно выше. Их вклад в общий баланс потерь энергии становится ощутимым, что'позволяет отнести указанные системы к коротким трубам.
Трубопроводы подразделяют на простые и сложные. Простыми трубопроводами называют системы только с последовательным соединением всех участков,* имеющих в общем случае разные параметры (о(,, 1,2 ). Сложные трубопроводы отличаются наличием разветвлений и параллельных линий. Простой и сложный трубопровод может быть разделен на ряд элементарных участков. Поэтому .естественно, что методика расчета проотых трубопроводов является основой для решения задач сложных систем.
Имеем напорную систему (рис. 3.12), включающую резервуар и простой трубопровод. Последний состоит из последовательно соединенных двух участков, имеющих разные диаметры. При работе системы, то еоть при вытекании жидкости в сечении 3-3, без учета потерь напора на сопротиг-ение можно принять, что в трубопроводе Цтсопвъ . Тогда 0 ^ 1Г2а>г - , или в общем виде
«/■А
где (5 и 1Г? - средняя скорость движения жидкости на участке и, И I, ; (А, и - площади живого сечения на этих участках.

А
| ти; |
| «Г, |
| на о ооью ' л |
I
| -с
|
Рио, 3.12. Напорная система из резервуара (А) и трубопровода (В). г'
Уравнение (3.34) называетоя уравнением неразрывности (сплошности) для потока жидкооти. Это одно из основных уравнений гидравлики, позволяющее достаточно просто устанавливать среднюю скорооть потока (напорного или ненапорного) в различных оечения)? как величину обратно пропорциональную их площади.
На ооновании уравнения (3.34) можно ооставить гависимос-
1,12
(3.1/5)
-Ц'^и^) - (3.36)
Составим уравнение Бернулли для потока жидкости в сечениях 1-1 (см. рис. ЗЛ2) и 3-3 (плоскость сравнения 0-0 совмеще-
оью трубы):
- 51 -
+ (3.36)
Следовательно, общий напор равен скоростному напору шгво потери энергии на сопротивление движению жидкости. Зависимозть (3.38) называется уравнением простого ^ р у бопровода. В общем случае действующий напор II - не только перепад геометрических высот системы. Он може-Д включать разность удельных работ сил давления в начальном и конечном сечениях, если давления в них не уравновешивают друг друга.
Для большинства случаев характерно значительное превышение действующего напора Н над скоростным напором в выходном сечении. Например, в водопроводных системах из экономических соображений обычно допускается скорость не выше 2-3 м/с, чему соответствует скоростной напор на выходе около 0,5 м. Действующий в системе напор Н чаще всего составляет десятки метров. Это дает возможность еще более упростить уравнение простого трубопровода, то есть пренебречь скоростным напором в выходном сечении:
Н-яК- ■ (3.39,
Зависимость (3.39) весьма показательна: в простом трубопроводе вся исходная энергия напора Н идет практически только на преодоление сопротивления по длине. Если движение в системе установившееся, то в общем случае на участках, где диаметр, расход и шероховатость труб одинаковы, его можно считать и равномерным. При этом потери энергии на трение по длине можно рассчитывать по формуле Дарси-Вейсбаха (3.22) или по формуле (3.30). С учетом последней уравнение простого трубопровода приводится к виду
Н=(в[1]/Х2)1; (3.40)
где О - расход (Лй) ; К - расходная характеристика
Уравнение простого трубопровода учитывает только потери энергии на трение пб длине. Статистический анализ показывает, что местные потери в трубопроводных системах обычно составляют исего 5-15!? от путевых. Тем не менее пренебрежение ими всегда падет к снижению скорости, а следовательно, и расхода при заданном напоре. Если это недопустимо, то в формулу потерь энергии по длине вводят поправочный коэффициент, суммарно учитываю-
щий местные потери энергии:
Н = (1.О?-М,15)«($1- (3.41)
Потери напора пошлине трубопровода, можно определить по уравнению, которое получено в результате преобразования уравнения Дарси-Вейсбаха 0.22):
Ь.-ЛЮ2, (3.42)
где А - удельное сопротивление трубы на 1 м при расходе воды I м3/о; определяется по формуле V . ^ ЗА
' (3.43)
где ^ - диаметр трубопровода, м.
Используя формулы (3,22) и (3.39), составляем уравнение
я V Т ■ (3.44)
По формулам (3,22) и (3.38) составляем уравнение проотого
трубопровода с учетом скоростного напора в выходном сечении Г2
1Г2 1Г*_*>(Х1 + 1)
(3.45)
Для короткого трубопровода, у которого потери напора по длине и местные потери соизмеримы (*Ь1«»*ЬМ), с учетом фор-, мул (3.22), (3 . 25) и (3.38) уравнение выглядит следующим обра-
30М: „ Л1Г* ** . *г гГг(ХI » _ с \
(3.46)
При необходимости в полученные уравнения (3.45) и (3.46) вводится величина коэффициента Кориолиса <4 , а в уравнение (3. 44) - поправочный коэффициент (1,05 + 1,15), суммарно учитывающий местные потери энергии (см. формулу 3.41), При гидравлических расчетах уравнения (3.44), (3.45) и (3.46) могут использо- ватьоя для определения параметров потока. Преобразуя эти уравнения, получимформулы определения скорости движения воды:
(3.47)
Мттшг,
Ы+и+хе,м<1 > (3.49)
или в обобщенном виде
«Г ' - (3.50)
где= ч - коэффициент скорости системы; <А - коэффициент Кориолиса; тб,' - коэффициент сопротивления системы, представляющий сумму коэффициентов всех потерь энергии (по длине и местных).
Расход трубопровода: а) в конечном сечении
в - у^^Н ; (3.51)
б) в конкретном сечении
\ (3.52;
где Н - напор в начале системы; и)- площадь сечения трубопровода (эго^А).
Преобразуя уравнения (3.44), (3.45) и (3.46), можно получить формулы определения других параметров потока жидкости в трубопроводах.
При проектировании новых трубопроводов могут быть неизвестны две величины - напор в начальной точке и диаметр. В этом случае задаются диаметром трубопровода в зависимости от расхода и рекомендуемых .(по экономическим соображениям) предельных скоростей по формуле
с1 -1.1?УЧ/Яч> . (3.53)
Предельные скорости зависят от величины расхода и материала труб. Для ориентировочных подсчетов при расходах от 2 до 3000 л/с можно принимать значения предельных окоростей для стальных труб от I до 1,7 м/с и чугунных - от 1,1 до 2,5 м/с. " Если в начале трубопровода напор создаетоя насосом, то
мощность последнего определится по формуле
#нПс 9.81-аНнАс/?, (3.54)
где К - коэффициент запаса на перегрузку двигателя: при ЛгАв< 1 кВт коэффициент К » 1,3; при М*1 ■= 1...50 кВт К - 1,2.. .1,05; 9,81 (<р) - ускорение свободного падения; 0 - подача насоса, м /о; Ни « - полный напор насоса, состоящий из гео-
метрической выооты подъема Ь = Нс«+а,к(где Нсв шР*/р% - овободный напор в конце трубопровода) и суммы потерь напора на всасывающем и нагнетательном трубопроводах; р - коэффициент полезного действия (КПД) насоса; КПД современных крупных центробежных насосов достигает 0,92, а мелких - 0,5...О,6.
Если высота всасывания и потери напора во всасывающей трубе незначительны, то напор ..асоса можно принимать как сумму высоты
нагнетания и потерь напора при нагнетании.
Пример 3.9. Напорная система из стальных труб 0,02) длиной I* Ю м и диаметром « 300 мм имеет два затво- проводу диаметром (I» 150 мм на расстояние I = 500 м. Определить: а) на какую высоту Ь в конце трубопровода будет пода- ватьоя вода при расходе 16 л/с; б) какой расход 0 будет в конце трубопровода на высоте Ь - 7м.
Решение. Определяем скорость движения воды в конце трубопровода по формуле (3.52)
"А016 = 0,91 м/с. «г**8 3,14-0,152
а)Определяем по формуле (3.22) потери напора по длине трубопровода, учитывая местные потери увеличением длины трубопровода на 10$:
и «1.12М1 = 1 р 1- 0,025-500-0,91 = 3 8? м< Пь <12$. 0,15-2-9,81
Следовательно, высота подъема будет равна
15 - 3,87 - 11,13 м. б) Определяем по формуле (3.48) скорость движения воды в трубопроводе на высоте Н ■ 7 м, считая Л,=М-И » 15 - 7 ■ 8 м и учитывая местные потери напора увеличением длинь^ трубопровода на 10$: _________
= Г^Ш:ШС.1,3 м/с.
у й + 1,Ш '0,15 + 1,1-0,025-500
Расход составит
- 1,30-3,14-0,152/4 « 0,023 м3/с » 23,0 л/с. П р и ме г)_ 3.16. Определить необходимый напор перед стальным (А = 0,02) дюкером диаметром ^ - 700 мм, длиной I = 500 м, проложенным под руслом реки для пропуска расхода: а) 0,5 м /с; б) 0,65 м3/с; в) 1,0 мЭ/с.,
Решение, а) Определяем'окорооть движения воды в коице дюкера по формуле (3.52)
у = а. ^0,5 1>3м/о.
3,14-0,7й
По формулам (3.22 и 3.25) определяем потери напора в дюкере и, следовательно, необходимый напор Л , учитывая, что коэффициент сопротивления при входе в трубу с острыми кромками составляет - 0,5: _
Ь 0.5-М- „ 1,27 м.
| - 58 - |
Пгр_Л " 42? 2%' 0,7-2 9,81 2-9,81 Решение (б) и (в) основано на зависимости между расходом, скоростью движения воды и потерями напора. Расходы и потери напора - функции скоростей, но потери напора прямо пропорциональны "вадрату окорооти. При увеличении скорости в п раз на отолько же -возрастает расход, а увеличение потерь напора происходит в п2 раз. Отсюда:
Дата добавления: 2015-04-18; просмотров: 238; Мы поможем в написании вашей работы!; Нарушение авторских прав |