
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Ц111Г1Г11,ЦТ>Г11>Г/'>ГЧ"1ТГ 2 страница
б) п, = йг/0а « 1,3 раза; Щ = «г * 1,27-1,32- 2,15 м.
в) пв=0в/0а - 2 раза; -На • » 1.27-22 - 5,08 м.
(2.^ 3.9. Гидравлический расчет фонтанов
^Прй'гидравлическом расчете фонтанов обычно определяют высоту фонтанной струи и расход воды в фонтану.
Из уравнения Д.Бернулли (3.16) известно, что скоростной напор = V1/** ; отсюда
(3.55)
где 1Г — скорость воды при выходе из насадка, м/с; Ь, - ско- роотной напор, м.
В результате сопротивления воздуха высота вертикального подъема струи несколько меньше скоростного напора (рио. 3,14):
(3.56)
■э
| [И |
а;
или с учетом
(3.57)
| Л |
где 1г а 0 - средняя окорооть и расход в выходном сечении; Н^ -I потерянный напор, вызванный сопротивлением воздуха; с( ~ диаметр выходного сечения ; ^ст^ - коэффициент сопротивления отруи.
1 I 1 ■
2Г
Рио. 3,14. К раочету еыооты подъема струи.
Для коэффициента сопротивления струи в свободном полете имеютоя различные эмпирические формулы. По Люгеру
= ън/О+кЮ, а (3.58)
где X - полный напор у выходного отверстия, Л = ; * -
коэффициент, равный ь 0.00025
'ТПОООЗ5"-' (3.59)
с/ - диаметр выходного отверстия, м.
Для ориентировочных расчетов, полагая 4ст!» * 0,1 получим
V 0,074 (ЧАг)\„ (3.60)
при О-в м3/о и в м.
Из формулы (3.57) получаем
• (3.61)
Преобразуя уравнение (3.56) с учетом, что ЬР = Ьв(1-^СтР), получаем формулу определения расхода в выходном сечении:
(3.62)
р
где а) - площадь выходного сечения, м .
По скоростному напору в выходном сечении можно определить величину манометрического давления (пьезометрическая вы- сотк р/уО, м вод. ст., перед насадком (рис. 3.14, сечение 1-1) по формуле
где - коэффициент сопротивления насадка. При раочетах
можно использовать следующие его числовые значения: для цилиндрического внешнего - 0,50; цилиндрического внутреннего - 1,0; конически сходящегося - 0,09; коноидального - 0,06; конически расходящегося при угле конусности 5-7° - 3,94-3,00.
По приведенным значениям коэффициентов сопротивления можно определить величину потерянной энергии (в процентах от напора):
(3.64),
Чаото насадок является концевым звеном трубопровода значительной протяженности, в котором происходят потери напора по длине и за счет наличия местных сопротивлений. Тогда скорость струи на выходе из насадка и раскод определяются по формуле
й~1Г(йн = ^ (** ' (3.65) |
где б - расход в выходном сечении, м/с; € - средняя скорооть движения воды на выходе, м/с; и)н - площадь выходного отверс-. тия насадка, м2; М - напор в начале системы, м;5„ас- коэффициент сопротивления насадка; - сумма коэффициентов меотных сопротивлений; А - коэффициент трения; I и с{- длина и диаметр трубопровода, м; с!и- диаметр выходного отверотия насадка, м.
Пример 3.17. Определить начальный напор системы, состоящей из резервуара и цилиндрического насадка диаметром в выходном сечении <1 = I см, если скоростной напор Ь„ « 3 м.
Решение. Определяем расход в выходном сечении по
формуле (3.62) 2 __________
а 31-3'-0,0006 М3/с
Из формулы (3.32) определяем начальный напор:
У __ _____ 0.00062__________ = 4 4 м
М = 1*2и)г2д. = 0,822-(7,85-10"д)г-2-9,81 Пример 3.18. От водонапорной башни ^ • 20 н о геодезической отметкой лг - 2 м проложен отальной ( > = 0,03) трубопровод диаметром с/ « 38 мм длиной I - 200 м, имеющий местные сопротивления - 6) и питающий фонтан с геодези
ческой отметкой а* « 5 м. Определить: а) высоту фонтанной отруи, если установлен цилиндрический насадок с диаметром (1и - 10 мм; б) потери напора в трубопроводе.
Решение, а) Определяем напор в начале системы:
Мн - Ь$ +3.6 - *ч> (* 20 + 2 - 5 « 17 м. По формуле (3.65) определяем скорость истечения струи из
насадка:
I------ &Н
,/ ~ 2-9,81-17 =12,08 м/с. ■
VI 7 0,5 + (6 + 0,03•200/0,038)(0,01/0,038)" Скоростной напор будет равен
12,08 /2-9,81 - 7,44 м. Для определения коэффициента .сопротивления отруи использу «м формулы (3.59) и (3.58): *
ь 0.00025 ........... 0,00025 п П?3.
+ 1000?? ~ 0,01 + 1000-0,013
' , - „0.023-,0,146.
Сстр \*кИ0 " 1 + 0,023-7,44 Высоту фонтанной струи определяем по формуле (3,56)
Кр=Ь0(1 ) - 7,44(1 - 0Д46) « 6,35 м.
б) Из условия неразрывности определяем скорооть движения поды в трубопроводе по формуле (3.35) - „ „ (А.\2312,08(-М!\10,84 м/с.
1ГтР-1' \о,038/
По формулам (3.22) (3.25) определяем потери напора по длине и местные потери:
и -0 -5,68 и;
<129 " * 0.03 .2-9,81
Т<Г 2-9,81
Общие потери напора в трубопроводе составят КР= + Ь„ = 5,68 + 0,22 = 5,9 м.
Проверка. Определяем пьезометрическую высоту перед насадком:
^ = 17 - 5,9 11,1 м.
Эту же величину определяем по формуле (3.63)
1 + ) - 7,44(1 + 0,5) - 11,16» 11,2 и.
<г
Следовательно, расчет системы выполнен правильно. К тому же с использованием формулы (3.64) по пьезометрической высоте перед насадком можно определить скоростной напор фонтанной струи. Тогда для цилиндрического внешнего насадка
и -Е - В.(. __________ ) » 11,1 - 11,1--------- = 7,4 м.,
п°~Г И 1 +«5"ПС / 1+0,5
9/ Водосливы
В практике гидротехнического строительства достаточно часто встречаются случаи перелива потока воды через какое-либо препятствие - порог, плотину и т.д. Теория движения жидкости через такого рода препятствия, называемые водосливгми, широко используется при расчете дорожных водопропускных труб, малых мостов, входных эле-ментов водопадов, порогов, каскадов, рао*одов поверхностного стока и пр,
.Преграда в потоке в виде стенки (порога), через которую осуществляется перелив жидкости, называется водосливом. Перед водосливом.происходит торможение потока, что сопровождается подъемом уровня и накоплением энергии, потребной для его преодоления. К водосливам относятся также сооружения, не имеющие порога, а стесняющие поток только в плане (малые мосты, трубы).
Поток может переливаться через водосливную стенку по всей ее ширине или же через вырез, сделанный в искусственном сооружении, который называется водосливным отверстием. Гребнем водослива называется линия, проведенная в пределах водосливного отверстия по точкам, имеющим в различных его поперечных сечениях'наибольшие отметки.
Часть потока, расположенная выше по течению от водослива, называется верхним б ь е ф о м, а ниже по течению - нижним бьефом.
| Ц> с? ЩН>№ |
| Нв = Л |
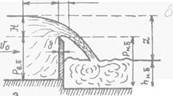
При подходе к водосливному отверстию скорость потока возрастает, а свободная поверхность понижается. Геометрическим (статическим) напором Я (рис.- 3,15) называется
(?-5)Л , 0.67Н
 тгтт
тгтт
|
' щтш/щтптшит
Рис. 3.15. Водосливы с тонкой стенкой, разница отметок гребня водослива и свободной поверхности перед ним на расстоянии (3 «■ 5)Я в сечении, где движение плав- ноизменяющееся и свободная поверхность имеет малую кривизну. Средняя скорость 1Г0 в этом сечении называется скоростью подхода. Полным напором (с учетом скорости подхода) называют величину ^
г% ' (з.бб)
Геометрический перепад а на водосливе представляет собой разность отметок свободной*поверхности в верхнем и нижнем бьефах в сечениях, где влиянием водослива на форму свободной поверхности можно пренебречь.
| (3.67) |
Водослив характеризуется следующими геометрическими размерами: шириной водосливного отверстия Ь , толщиной стенки водослива? , высотой порога водослива Р.(со стороны верхнего бьефа Ре 5 и нижнего - Рн.5 ), Глубиной подтопления называют разность отметок уровня воды в нижнем бьефе и гребня водослива (рис. 3.15; 5):
Ь* =* Ь„.5 - Рм.5
По форме и относительной толщине стенки, определяющих характер перелива потока, водосливы подразделяются на: водосливы с тонкой отенкой, водооливы о широким порогом и водосливы практического профиля.
Водосливы с тонкой стенкой (ом. рио. 3.15), при переливе через которые струя отрывается от верхового ребра гребня. Толщина стенки не оказывает влияния на форму струи ($/N^0,67).
Водосливы с широким порогом
(рио. 3.16,а) . При переливе через них на среднем участке греб-
Ь-сВ
| ШИШШ» | |||
| Я} | __ | • | |
^ Рис. 3.16. Виды водосливов, ня 1ег движение становится плавноизменяющимся, тогда как на участках входа 1«ж и слива I.* поток является резкоизменяю- щимся, Это имеет место при толщине порога Ь/м > (2 ♦ 3). Обычно к водосливам с широким порогом относят водосливы, у кото-" ры> (2 ♦ 3)<1/Н<В . Однако многие дорожные водопропускные сооружения, например безнапорные трубы, при относительных длинах Ь/Я * 50 работают по схеме истечения через водослив о широким порогом.

|

|
Водосливы практического профиля (рис, 3.17) занимают промежуточное положение и харак-
 Рис. 3.17. Водослив практического профиля.)
теризуются отношением 0,б7<8/Д« (2'+ 3).
По характеру сопряжения с нижним бьефом водосливы делятся на:
неподтопленные (см. рис. 3.15,а), когда параметры потока в нижнем бьефе не оказывают влияния на про-' пуокную способность водослива;
подтопленные (см. рис. 3.15,!" ), когда пропускная способность изменяется с изменением уровня воды в нижнем бьефе.
По соотношению ширины водослива Ь и подводящего русла В водосливы (см. рио. 3,16) делятся на водосливы без бокового сжатия (О и водосливы о боковым
Рис. 3.17. Водослив практического профиля.)
теризуются отношением 0,б7<8/Д« (2'+ 3).
По характеру сопряжения с нижним бьефом водосливы делятся на:
неподтопленные (см. рис. 3.15,а), когда параметры потока в нижнем бьефе не оказывают влияния на про-' пуокную способность водослива;
подтопленные (см. рис. 3.15,!" ), когда пропускная способность изменяется с изменением уровня воды в нижнем бьефе.
По соотношению ширины водослива Ь и подводящего русла В водосливы (см. рио. 3,16) делятся на водосливы без бокового сжатия (О и водосливы о боковым
|
ожатием (8).
| 1ДВДМ |
По форме выреза в стенке (рис. 3,18) водосливы подразделя-
| в . | ||
а 5 8 2
,Рио. 3.18. Виды водосливов по форме выреза в стенке
ютоя на прямоугольные («^треугольные ( ? ) ; трапецеидальные («^круговые ( 3) и другие.
По очертанию стенки в плане водосливы делятся на прямолинейные (рис. 3.19): нормальные (а); косые (г) и непрямоли-

|
5 в 2 4
Рис. 3.19. Виды водосливов по очертанию стенки.
нейные: ломаные (б); криволинейные (9); кольцевые (а).
По высоте порога различают водосливы с порогом, когда Р> О ,, и водосливы без порога, когда Р-о. Например, протекание поды через отверстие малого моста может трактоваться как истечение через водослив с широким порогом, высота которого Р-§__)• Ооновная формула для расчета водосливов всех типов имеет
вид .
. О . тЪЩП? = тЬЯ^Го.^ (3.68)
При малой скорости подхода, если 1Гв< I м/с, что бывает При (А* г>4ЬН , формула определения расхода принимает вид
ГДв(« } безразмерный коэффициент расхода, различный для разных типов водосливов и для различных условий их работы.
Для предварительных расчетов могут быть приняты следующие значения коэффициента пг для неподтопленных водосливов: водос- лии 0 тонкой стенкой (с стрым гребнем) - 0,42; водосливы практического профиля: безвакуумный - 0,45; вакуумный - 0,50; ПодООЛИВ о широким порогом - 0,35. Уточненные значения коэффициента т указаны в работе [2Я •
| Расход водослива треугольной формы с тонкой стенкой, ее-
ли центрапьный угол л = 901', определяется по формуле Томпсона: М,^ , м3/о (3.70)
Основной формулой расхода трапецеидального водослива можно считать формулу
й - - (3.71)
где оь — угол между боковой наклонной кромкой и вертикалью.
Для трапецеидального водослива в тонкой стенке при угле А = 14° (или, точнее, при коэффициенте откоса боковой его кромки, равном 0,25) в том случае, если длина его порога Ь?4Л , расход^ может определяться по формуле
й^тЬЛ^Н, (3.72)
причем коэффициент расхода "» = 0,42 принимается постоянным, не зависящим от напора Л .
Особенности движения воды через водосливы используются при расчетах шахтных и трубчатых водосбросов, приемная часть которых устраивается в виде водосливной воронки (кольцевого водослива).
При отсутствии противоводоворотных устройств на кодосливе и отсутствии его подтопления за счет последующего за воронкой напорного водосбросного тракта расход определяется по формуле 0 = т2т-КнУ2р'> (3.73)
где К - радиус водосливной воронки, м.
При этом коэффициент расхода определяется по формуле
т = О,94[0,49О-О,О68(^]. Л ^
Обычно при расчетах водосброоов известен расход воды, по которому рассчитывается радиус воронки водосброса. Преобразуя уравнение (3.73), получаем формулу определения радиуса водоо- лИЪной воронки:
К= ^2x3ЬфГ ' М- (3.75)
Диаметр вертикальной трубы за воронкой определяется по - | формуле ,
(3.76) |
где IГи- скорость движения воды, определяемая по формуле
Т/у- 0,93 (3.77)
где у - вертикальное расстояние от гребня водослива до сечения, в котором определяется скорость потока.
Радиус поворота оси колена (сопряжение с горизонтальной трубой) принимается в пределах (2 +■ 5)с^ , где диаметр вертикальной трубы.
Пример 3.19. Определить ширину прямоугольного водо- олива о тонкой стенкой для пропуска через него расхода 0 а 50 л/с при напоре Я * 0,2 м и свободном истечении. Высота порога водослива Р«.« « Рн ь -0,5 м, глубина воды в нижнем бьефе ЬнЬ " 0,35 м, боковое сжатие отсутствует.
Репе н и е. Устанавливаем, является ли водослив подтопленным или неподтопленным. При р - водослив не подтоплен. Ширину отверстия водослива находим по формуле (3.69), используя значение коэффициента расхода т » 0,42:
ь в_________ ___________ 0.05 _п з
~ ~ 0.42-0,2^-9,81-0,2'" '
Пример 3.20. Найти напор перед прямоугольным водоо- ливом в тонкой стенке шириной Ь I м, если й« 0,2 м3/с, Р = 1 м, Ьн.* * 0,8 м при отсутствии бокового сжатия.
Решение. Так как Р>Нн.% , устанавливаем, что водо- олив не подтоплен. Напор перед водосливом найдем из формулы 0.69)
м я х (_______ = 0,23 м.
Пример 3.21. Определить расход воды через треугольный водослив с центральным углом 90°, если напор воды Л - 12 мм.
Решение. Расход воды устанавливаем по формуле (3.70)
й - 1,4Лг/ЗГ- 1,4-0,0122У0,012 - 2,21-10""5И/о»0,022 л/с.
Пример 3.22. Определить раоход воды через незатоп- , ленный трапецеидальный водослив о тонкой отенкой при ширине порога Ь = 0,5 м и напоре Н = 0,2 м, если угол между боковой кромкой водослива и вертикалью ^ - 20°.
Решение. Расход определяем по формуле (3.71), предварительно установив по таблицам тригонометрических функций, что 20° » 0,364:
й + ' 0,42(0,5 + 0,8-0,364-0,2)-
О,2^2-9,81-0,2'' 0,093 м3/о.
Пример 3.23. Определить раоход воды через прямоугольный водослив о тонкой стенкой при ширине Ь = 1 м, напоре Л • 0,5 м, еоли водослив не подтоплен, а площадь сечения потока в верхнем бьефе Ав.ь » 2 м2.
Решение. Поскольку не известен расход и скорость
подхода, определяем расход по формуле (3.69), то есть без учета окоростного напора:
«ЬЛ /23ЗГ- 0,42-1-0,5/2-9,81-0,5 ■ 0,658 м3/о. Определяем скорость подхода V, по формуле 1Г0 =0/«>в.5 - В,658/2 - 0,33 м/с.
По формуле (З.Г.6) определяем напор на водосливе с учетом окоростного напора при «с - I:
V » 0.5 + 1"°>33 = 0,51 м.
0 2* 2-9,81
С учетом окоростного напора раоход водослива по формуле (З.бЬ) ооставит
О - тЬ Л./Щ1- 0,42-1-0,51/2-9,81-0,51 » 0,678 м3/о. Повторно определяем скорость подхода 6Г„= 0,678/2 - 0,34 м/с и напор на водосливе с учетом скоростного напора:
Л, -0,5 + 0»3'* = 0,51 м. 4 2-9,81
Поскольку напор на водосливе Нв в обоих случаях одинаков, расход водослива будет 0,678 м3/с.
Пример 3.24. Определить радиус сливной воронки и
диаметр вертикальной части трубчатого водосброса о раоходом в»
0,5 м3/о при напоре И » 0,25 м и высоте вертикальной чаоти у» 5 м.
Решение. По формуле (3.74) определяем коэффициент, раохода, принимая предварительно К' 0,2 м:
т =0,94[0,490 - 0,068(|-)^] =
0,94 [о,490 - 0.068(0х2|)*] ,0,3?.
Определяем радиуо воронки по формуле (3.75)
С ® - 0.^ о 37 м
тг-гНЯяУГ 0,39-2-3,14-0,25/2-9,81-0,25' " '
Уточняем значение коэффициента расхода
| К |
т *0,94[0,490 - О.Обб^Щ)^] = 0,40. Повторно определяем радиус воронки
0,5
====—^ =* 0,36 м.
"и.ч-СО.М. 0,25/2-9,81-0,25'
ЭНаЧ6НИЯ РВДИЗГ°а В0Р°НКИ В °б0ИХ п.ч™ не от
личаются, расчет прекращаем, принимая Я = 0 36 м
Определяем скорость движения воды в конце вертикальной
чаоти водосброса по формуле (3.77)
15= 0,93У2$$Г = 0,93т/2-9,81- 5 9,21 м/о. По формуле (3'.76) определяем диаметр вертикальной части водооб-
рооа _______________________________________
<1 = т/4 О/я V; ' т/4 - 0,5/3,14-9,2? = 0,26 м. Поокольку ближайшие стандартные размеры труб равны 250 и 300 мм, принимаем больший из них при устройстве вертикальной части водосброса. В противном случае возможно подтопление во- доолива и уменьшение его расхода, что повлечет за^ собой подъем уровня воды в водохранилище выше'допустимого.
Форма поперечного сечения каналов может быть прямоуголь-

|
3,11. Гидравлический расчет каналов
Рио. 3.20. Форма поперечного сечения каналов, ной (в), округлой (г), треугольной и др.
„ Форму сечения канала принимают в зависимости от его назначения, размеров и способа производства земляных работ. Открытые искусственные каналы мелиоративных' и водных систем обычно имеют трапецеидальное сечение, а дренажных - округлое. Каналы (лотки) небольших расходов, изготовленные из искусственных материалов, как правило, имеют прямоугольное сечение.
При гидравлическом расчете каналов определяются их размеры, на основании которых вычисляются необходимые характеристики потока. Основные элементы потока рассмотрены в разделе 3.2 ( и) - площадь живого сечения потока, м2; х - смоченный периметр, м; й - гидравлический радиус, м; 0- расход воды^или пропуокная способность канала, м /с; \Г - средняя скорость потока, м/с).

|
Приняты следующие об значения (рис. 3.20): В - ширина ка-* нала поверху или, точнее, ширина водной поверхности, м; Ь- ширина по дну, м; Ь - глубина воды в канале, м; I - проекция откооа канала, м ; - угол откоса; т- коэффициент откоса
(коэффициент заложения откооа). Кроме того, при расчетах определяется уклон канала (») и устанавливается коэффициент шероховатости русла
Коэффициент откоса («) - это с^Л , или отношение проекции откооа к глубине (1/к). Коэффициент откоса обычно кратен 0,25 и меняется от 0,25 до 5,0. Коэффициент заложения откосов зависит от назначения канала и рода грунта (табл. I, Приложение).
Кивое сечение потока в каналах, смоченный периметр и гидравлический радиус определяют по следующим формулам:
а) для прямоугольного сечения (рис. 3.20,я): а) ~ЬН ;
о-А ьь ■ к'х " ь+гь '
.8 = Ь;
б) для равнобокого трапецеидального сечения (рис.3.20,5): й> ж (Ъ + тк)к - Ьк + тк2 ; (3.82)
ь+гь^ + т*-, * (3.83) р Л. - ЬЬ +• т Ь2
К~ *> Ь+йкт/Г+т*' ' (3.84)
В - Ь 2тЬ ; (3.85)
| при при |
| (3.86) |
в) для сложного трапецеидального поперечного профиля (рис. 3.20,в):
Л, «Ыц+щ.Ь* И «Д, = (6 ^а**»^ ;
* = Ж,
(3.87)
, В,,=Ь*2т,к1 и. В2-=Ь*2т,Ь, +2т2Ь1 ; (3.88)
г) для круглого сечения при полном его заполнении (рис. 3.20,2):
4} (3.89)
(3.90)'
К Т - (3.91)
В садово-парковых объектах возможны случаи устройства каналов с разной крутизной откосов, когда один из них укрепляется облицовкой и поэтому имеет меньший коэффициент откоса. При разной крутизне откосов площадь сечения
| (3.78) (3.79) (3.80) (3.81) |
и) = (Ь + 1г>ег к) Ь , (3.92) 1
где /п<„ » омоченный периметр
+ (3.93)
ширина русла по свободной поверхности потока
В = Ь^2тСрЬ. (3.94)
Уклоном канала называется отношение падения канала по дну &Н к его длине I (указанные величины должны быть в одних единицах длины) О или 1= (Нистока - Нустья)/Ь . где
"иотока " абсолютная^ (относительная) высот^ истока канала; ^устья ~ то же Уотья канала- Уклоны выражаются в десятичных Дробях и промилле. Например, уклон канала равен 0,0005, что в промилле соответствует 0,5%>, то есть на 1 км длины канала падение составляет в среднем 0,5 м.
Для определения средней скорости потока при равномерном движении жидкости пользуются^фо^мулой Шези (3.26):
гг = ОШ,
0 5
где С - коэффициент Шези, м ' /с.
Коэффициенты С являются общей характеристикой сопротивлений естественных русл, включая местные сопротивления в виде изменений формы сечения по длине потока, локальных размывов, крупных подводных камней, поворотов и т.д. 8 подавляющем большинстве случаев, омоченные поверхности каналов и естественных руол можно считать абсолютно шероховатыми. Коэффициент Шези для этой облаоти сопротивлений определяют по эмпирической фор муле, предложенной акад. Н.Н.Павловским:
С = ««У> (3.95)
где п- коэффициент шероховатости; его значения приведены в приложении (табл. 2);
Для предварительных расчетов можно полагать У ■ 1/6 (по Маннингу) или у = 1/5 (по Форхгеймеру). Для уточненных расчетов рекомендуется полная формула Н.Н.Павловского:
У - 2,5У>Г- 0,13 - 0,75Уп (УК* - 0,10), (3.96)
вычисленные по которой коэффициенты С приведены в приложении (табл. 3).
Используя значения коэффициента С и средней скорости V , можно определить: расход воды ((5) по формуле (3.28), скорост ную характеристику (1г) по формуле (3.27) и расходную характеристику ОС) по формуле (3.29).
Каналы, сечение которых при неизменной площади о>0 характеризуется наименьшим значением омоченного периметра хты и, следовательно, наибольшим значением гидравлического радиуса Кто.*' • согласно формуле Шези (3.26) обладают наибольшей пропускной,^способностью при равномерном движении. Такое оечение канала называется гидравлически наивыгоднейшим (/»„«). Для каналов прямоугольной формы поперечного сечения характеризуется равенством 6" 2к, а для каналов трапецеидальной формы - рг.н ■ Ь/к = 20Л + т2'-т).
^'Значения ргч -Ь/Ьдля гидравлически наивыгоднейшего сечения трапецеидального канала:
« 0 0,25 0,50 0,75 1,0 1,25 1,50 1,75 2,0 3,0 4,0 5,0 Рг.« 2 1,56 1,24 1,0 0,83 0,70 0,61 0,53 0,47 0,32 0,25 0,20
Из этой зависимости следует, что канклы с гидравлически наивыгоднейшим сечением являются относительно глубокими. Поэтому проектировать крупные каналы с рги не всегда экономически целесообразно. Например, у судоходного канала шириной Ь * 100 м при ргм = 2 глубина к » 50 м. Глубина же канала в этом случае должна, назначаться исходя из осадки судов. Малые же каналы целесообразно проектировать с гидравлически наивыгоднейшим сечением, которое оказывается и экономически наивыгоднейшим в случае устройства канала с дорогостоящей облицовкой его дна и боковых откосов.
Одной из задач, решаемых при гидравлическом раочете ка-* налов, является определение средней скорости потока V и пропускной способности канала (расход воды)^0р, если известны размеры канала {Ь, к и т), у клон .'поверхности воды I и коэффициент шероховатости п . Предварительно по соответствующим формулам вычисляют площадь живого сечения й>, гидравлический радиус К , коэффициент С и потом по формуле Шеви (3.26) определяют скорость гГ, а по формуле (3.28) - расход воды 0 .
Иногда гидравлическим расчетом требуется определить уклон { по заданному расходу 0 , размерам канала и коэффициенту п . Из формулы (3.28) искомая величина уклона I- с О*/<х?02К .
| - 72 - |
При проектировании каналов довольно часто встречаются случаи, когда известен расчетный расход воды 0Р> и гидравлическим расчетом необходимо установить отдельные параметры какала для пропуска ()р . Например, требуется рассчитать размеры поперечного сечения канала, то есть глуби1 \Ук и ширину Ь при известных О, ь, 1. Так как здесь неизвестными величинами являются Ь и И , то одной из них задаются, а вторую определяют.
Задачу решают графоаналитическим способом или при помощи специальных вспомогательных таблиц либо графиков. Для решения задачи графоаналитическим способом при назначенной, например, ширине канала по дну Ь задаются рядом значений (тремя или четырьмя) глубины Ь и находят ей, х , Я , С,Х. Вычисления рекомендуется делать в табличной форме: ^
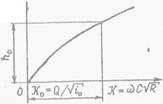
| Рис. 3.21. График к расчету нормальной глубины ,роды в канале. |
г........... = ... :'у.м i "*"",м ЗГ^С^м3/0
По значениям расходной характеристики и глубинам строят кривую зависимости Х=Х(И), которая должна проходить через начало координат (рис. 3.21) < Ь I
| ь | ||
| -а | ||
Рис-. 3.22. График к расчету ширины канала по дну: 1 - для трапецеидального сечения ; 2 - для прямоугольного сечения.
По этой кривой, отловив на оси X заданную расходную характеристику ЭС0=а/-/Г7 , определяют искомое значение и проверяют его вычислением расхода воды по формуле (3.28). При равномерном движении уклон дна канала 10 -- <• . Затем подсчитывают скорость тГ= / Глубину потока при равномерном движении жидкости называют нормальной глубиной.
Если глубину подбирают непосредственно по расходам воды, то в приведенную выше табличную форму вместо графы К вводят
графы -/Г, 1? и 0.
Если назначена глубина Ь , то Ь вычисляют аналогично,
заменяя в таблице графу Ь графой Ь . При этом надо иметь в виду, что в общем случае ривая X =7С(Ь) проходит не через начало координат (рис. 3.22),Ь,<Ьг,
3.12. Морфологическая характеристика и о) гидрологический режим рек
Реками называются водные потоки, питающиеся стоком вод атмосферных осадков и протекающие в выработанных ими руслах с односторонним уклоном.
 Рис. 3.23. Бассейн реки и речная система: ^-Ш - пбрядок притоков; В - водораздел.
Совокупность всех рек данной территории образует речную сеть, которая является частью гидрографической сети той же территории. Гидрографическая сеть включает все поверхностные водные объекты: реки, озера, водохранилища, болота.
Начало реки называется истоком, место впадения ее в море, озеро или другую реку - у с т ь е м. На протяжении от истока до устья река течет вречной долине - это относительно узкое, вытянутое углубление речного бассейна. _Левь'й Уерег * " Правый 5ерег
Бровка долины
Рис. 3.23. Бассейн реки и речная система: ^-Ш - пбрядок притоков; В - водораздел.
Совокупность всех рек данной территории образует речную сеть, которая является частью гидрографической сети той же территории. Гидрографическая сеть включает все поверхностные водные объекты: реки, озера, водохранилища, болота.
Начало реки называется истоком, место впадения ее в море, озеро или другую реку - у с т ь е м. На протяжении от истока до устья река течет вречной долине - это относительно узкое, вытянутое углубление речного бассейна. _Левь'й Уерег * " Правый 5ерег
Бровка долины
|

Дата добавления: 2015-04-18; просмотров: 217; Мы поможем в написании вашей работы!; Нарушение авторских прав |