Уравнение Бернулли. Движение жидкости в потоке сопровождается взаимным превращением различных видов механической энергии

Движение жидкости в потоке сопровождается взаимным превращением различных видов механической энергии. Например, при сужении потока его скорость, а следовательно и кинетическая энергия увеличивается, а давление и потенциальная энергия уменьшаются. Уравнение, описываю-

щее эти превращения, называется уравнением Бернулли и для потока идеальной жидкости имеет следующий вид:

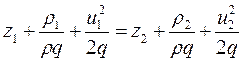, м, (5.1)

где z – высота положения;

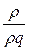- пьезометрическая высота;

- скоростной напор.

Так как все слагаемые уравнения (3.9) имеют линейную размерность, то их можно изобразить графически (рис.5.1), что даёт наглядное представление об изменении различных видов удельных энергий при переходе от одного сечения к другому.

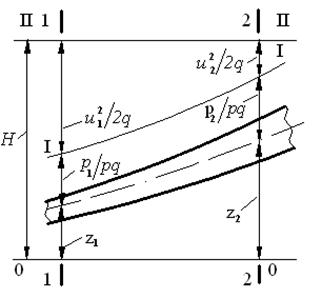
Рис. 5.1: 00 – плоскость сравнения;

I-I – пьезометрическая линия;

II-II – напорная плоскость;

Н – полный гидродинамический напор.

Анализ графиков рис. 5.1 показывает, что напорная плоскость II – II проходит параллельно плоскости сравнения, а полный гидродинамический напор Н = const. Из проведённого анализа следует, что при движении идеальной жидкости её полная механическая энергия не изменяется.

Однако, широко используемые в технике жидкости, такие как масло, вода и др., по своим свойствам близки к реальным жидкостям, в которых при движении между частицами возникают силы трения. При движении такой жидкости её удельная энергия уменьшается, так как она частично расходуется на преодоление силы трения. С учётом потерь напора на трение уравнение Бернулли (5.1) для потока реальной жидкости будет иметь следующий вид:

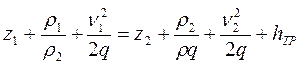, (5.2)

где h_TP – потери напора на трение, м.

Потери напора на трение численно равны гидравлическим сопротивлениям, которые в зависимости от природы их проявления подразделяются на два вида:

- сопротивления по длине;

- местные сопротивления.

Сопротивления по длине проявляются по всей длине участков труда, а местные сопротивления обусловлены различными конструктивными элементами, создающими препятствия движению жидкости (кран, вентиль, поворот потока и т.п.)

На рис. 3.4 показан участок трубопровода, на котором обозначены коэффициенты сопротивлений местных и по длине. В соответствии с видами гидравлических сопротивлений потери напора h_TP также подразделяются на потери напора по длине h_L и местные потери h_M [6] .

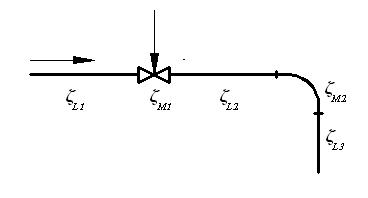
Рис. 2.4: 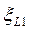, , 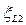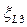- коэффициенты сопротивления по длине;

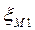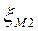, - коэффициенты местных сопротивлений

В гидравлических расчётах используется принцип наложения потерь:

h_TP = 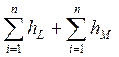(5.3)

На практике определение h_TP осуществляется по уравнению Бернулли, или по формуле Байсбаха. При равномерном движении жидкости (v₁₌ v₂) и горизонтальном трубопроводе (z₁ = z₂) из уравнения Бернулли получим:

h_TP = 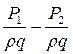(5.4)

Отметим, что при небольших напорах давления P₁ и P₂ в уравнении (5.1) можно измерить пьезометром.

В проектных расчётах h_TP обычно определяют по формуле Байсбаха:

h_TP = (5.5)

Формулы Байсбаха для определения потерь напора местных и по длине отличаются одна от другой только индексами при h и :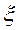

, (5.6)

(5.7)

Местный коэффициент сопротивления является технической характеристикой данного сопротивления и определяется по справочным таблицам.

Коэффициент сопротивления по длине ξ_L в формуле (2.15) зависит от коэффициента сопротивления трения λ (коэффициента Дарси). Эта зависимость устанавливается формулой (5.8):

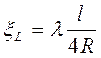, (5.8)

где l - длина участка трубопровода, м;

R - гидравлический радиус трубы, м.

Для трубопровода круглого сечения с учётом формула (5.8) будет иметь следующий вид:

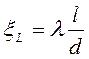, (5.9)

где d – диаметр трубы участка трубопровода.

Подставив (5.9) в выражение (5.7) получим общую формулу для определения потерь напора на преодоление сопротивления по длине в круглой трубе:

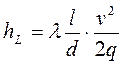(5.10)

Расчёт значений коэффициента сопротивления трения 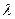осуществляется по эмпирическим формулам в зависимости от вида движения жидкости, определяемого числа Рейнольдса Re:

Re = 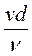, (5.11)

где - коэффициент кинематической вязкости.

Из курса физики известно, что переход ламинарного движения в турбулентное в круглой трубе осуществляется при Re_кр = 2320.

Если Re< 2320, то режим движения ламинарный и коэффициент сопротивления трения 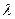определяется по формуле (5.12):

(5.12)

При Re > 2320 используется формула (5.13):

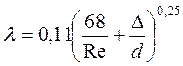, (5.13)

где 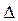- шероховатость стенки трубы, м.

Уравнение Бернулли для потока реальной жидкости (5.2) используется при расчётах гидравлических систем перекачки. Так, если в системе имеется насос, то требуемый напор насоса Н_н можно определить из уравнения (5.2), записав его в разностном виде:

Н_н = 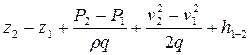(5.14)

где 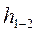- потери напора в трубопроводе на участке 1-2. Разностью скоростных напоров в уравнении (5.14) на практике часто пренебрегают, так как скорости движения жидкости в трубопроводе малы и отличаются они на концах участка 1-2 незначительно. В этом случае (5.14) примет более простой вид:

Н_н = 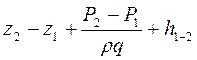(5.15)

Отметим, что основными характеристиками гидравлического насоса, по которым осуществляют его выбор, являются напор Н_н, м и подача

Q, м³/с.