Задание. 1. Определить силу и центр давления воды на плоскую стенку

1. Определить силу и центр давления воды на плоскую стенку

2. Построить эпюру давления с обозначениями центра давления

Задание:

По исходным данным, приведенным в таблице 1 приложения 1 для соответ­ствующего варианта, требуется определить силу и центр давления воды на плоскую стенку шириной b (м), с углом наклона αпри рас­положении воды с одной стороны стенки. Высота столба воды перед стенкой — Н (м)

Построить эпюру давления с обозначением центра давления.

Рис.1. Схема плоской стенки

При расчете некоторых гидротехнических сооружений необхо­димо найти давление жидкости на плоские прямоугольные стенки, щиты, задвижки и определить центр приложения этого давления.

Направление силы давления жидкости на плоскую стенку со­гласно первому свойству гидростатического давления всегда перпен­дикулярно к плоской стенке.

Величина давления на плоскую фигуру определяется по форму­ле

Р = ρgh_cw, (1)

ρ - плотность жидкости, кг/м³;

h_c - глубина погружения центра тяжести фигуры от свободной поверхности на вертикали, м;

w- площадь рассматриваемой фигуры, м²;

g- ускорение свободного падения, g = 9,81 м/с².

Точка приложения силы Р на плоскости фигуры называется центром давления. Расстояние по вертикали от свободной поверхности до центра давления определяется по формуле:

h_д = h_c+ 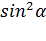, (2)

где h_с — расстояние по вертикали от свободной поверхности до центра тяжести фигуры, м;

Iс — момент инерции фигуры относительно горизонтальной оси, проходящей через центр тяжести, м⁴;

α — угол наклона фигуры (стенки) к горизонту;

𝜔—смоченная площадь фигуры (стенки), м².

Расстояние от свободной поверхности до центра давления по стенке определяется по формуле:

Y_Д = Yc+ (3)

где Yc — расстояние от свободной поверхности до центра тяжести фигуры, м.

Момент инерции плоского прямоугольника относительно горизонтальной оси, проходящей через его центр тяжести, определяется по формуле:

Ic = , (4)

b - ширина стенки, м;

у — длина наклонной стенки, м.

Для плоской фигуры круглой формы

I_C = r (5)

r- радиус круга , м.