
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Виды гидравлических сопротивлений
Рассмотрим последнее слагаемое в уравнении Бернулли h1-2 – потери напора на гидравлических сопротивлениях. Существует два вида гидравлических сопротивлений – потери напора на местных сопротивлениях hм и потери напора по длине (потери напора на трение) hд (hтр). Потери напора на местных сопротивлениях происходят тогда, когда резко меняется величина и направление средней скорости. Считается, что потеря напора происходит в том поперечном сечении, где изменяется скорость. Потери на местных сопротивлениях рассчитываются по формуле Вейсбаха:
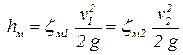 , ,
| (4.1) |
где v1 – скорость до местного сопротивления;
v2 – скорость после местного сопротивления;
zм1 – коэффициент местного сопротивления, рассчитанный по скорости v1;
zм2 – коэффициент местного сопротивления, рассчитанный по скорости v2.
Коэффициенты местных сопротивлений zм1 и zм2 не имеют размерности и связаны соотношением:
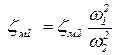 , ,
| (4.2) |
где w1 и w2 – площади поперечных сечений до и после сопротивления.
В большинстве случаев потери напора на местных сопротивлениях находятся по скорости после местного сопротивления v2. Но есть исключения: потери напора на выход жидкости из трубы в бак и потери напора на резкое расширение потока рассчитываются по скорости до местного сопротивления v1. В таблице приведены некоторые местные сопротивления и значения местных сопротивлений:
Таблица 1
| Вход в трубу | Резкое расширение | Выход из трубы | Выход в атмосферу |

| 
| 
| 
|
| zвх = 0,5. |  . .
| zвых = 1,0. | zвых.ат = 0,0. |
| Для следующих местных сопротивлений коэффициенты находятся по справочникам | |||
| Поворот трубы | Резкое сужение | Вытяжной тройник | Приточный тройник |

| 
| 
| 
|
Рассмотрим горизонтальный участок трубы, заполненный жидкостью (рисунок 4.1). Если жидкость в трубе не движется, то ее взаимодействие со стенками приводится к одной равнодействующей, направленной вниз (вес жидкости). При движении жидкости между нею и стенками трубы возникают дополнительные силы сопротивления, в результате чего частицы жидкости, прилегающие к поверхности трубы, тормозятся. Это торможение вследствие вязкости жидкости передается следующим слоям, причем скорость движения частиц по мере удаления от оси трубы постепенно уменьшается. Равнодействующая сил сопротивления направлена в сторону, противоположную движению, и параллельна направлению движения. Это и есть силы гидравлического трения (сопротивления гидравлического трения).
 Рисунок 4.1 - Распределение– распределение скорости в трубе. Рисунок 4.1 - Распределение– распределение скорости в трубе.
|
Для преодоления сопротивления трения и поддержания равномерного поступательного движения жидкости необходимо, чтобы на жидкость действовала сила, направленная в сторону ее движения и равная силе сопротивления, т. е. нужно затрачивать энергию. Необходимые для преодоления сил сопротивления энергию или напор называют потерянной энергией или потерями напора.
Потери напора, затрачиваемые на преодоление сопротивления трения, носят название потерь напора на трение по длине или потерь напора по длине потока (линейные потери напора) и обозначают hтр. Потери напора на трение рассчитываются по формуле Дарси-Вейсбаха:
 , ,
| (4.3) |
где l - коэффициент гидравлического сопротивления трения;
l – длина участка трубы;
D – внутренний диаметр трубы.
Из формулы (3.33) следует, что потеря напора на трение по длине при движении жидкости в трубе возрастает с увеличением средней скорости потока и длины рассматриваемого участка трубы и обратно пропорциональна ее диаметру. Кроме того, в эту формулу входит неизвестный безразмерный коэффициент l (так называемый коэффициент гидравлического трения).
Следовательно, потери напора при движении жидкости складываются из потерь напора на трение и потерь напора на местные сопротивления, т. е.
 , ,
| (4.4) |
Определение потерь напора при движении жидкости является одной из важнейших задач гидравлики.
Дата добавления: 2015-04-18; просмотров: 1105; Мы поможем в написании вашей работы!; Нарушение авторских прав |