
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вязкость
Вязкость – это свойство жидкости оказывать сопротивление сдвигающим усилиям. Вязкость - свойство, присущее как капельным жидкостям, так и газам, которое проявляется только при движении, не может быть обнаружено при покое, и проявляется в виде внутреннего трения при перемещении смежных частиц жидкости. Вязкость характеризует степень текучести жидкости и подвижности ее частиц. Вязкостью жидкостей объясняется сопротивление и потери напор, которое возникает при движении их по трубам, каналам и прочим руслам, а также при движении в них инородных тел.
Изучение свойств внутреннего трения жидкости активно занимался Исаак Ньютон, заложив основы учению о вязкости. Ньютон высказал предположение (впоследствии подтвержденное опытом), что силы сопротивления, возникающие при таком скольжении слоев, пропорциональны площади соприкосновения слоев и скорости скольжения. В итоге, И.Ньютон получил зависимость, характеризующую связь вязкости с явлением внутреннего трения, получившую название одноименного закона.

Рис. 1.2. Распределение скоростей при течении жидкости вдоль плоской стенки
Пусть жидкость течет вдоль плоской стенки параллельными слоями. Каждый слой будет двигаться со своей скоростью, причем скорость слоев будет увеличиваться по мере отдаления от стенки.
Рассмотрим два слоя жидкости, движущиеся на расстоянии Δy друг от друга. Поскольку между слоями присутствует сила трения и благодаря взаимному торможению различные слои имеют различные скорости, и слой А движется со скоростью v, а слой Б – со скоростью (v+Δv). Величина Δv является абсолютным сдвигом слоя А по слою Б, а величина Δv/Δy – относительным сдвигом, или градиентом скорости. Тогда при движении возникает касательное напряжение τ (тау), которое характеризует трение на единицу площади (напряжением внутреннего трения). Напряжение внутреннего трения имеет физический смысл зависимости:
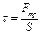 ,
,
где Fтр – сила внутреннего трения, Н; S – площадь соприкосновения поверхностей, м2.
Тогда согласно закону Ньютона зависимость между напряжением и относительным сдвигом будет иметь вид:
 ,
,
т.е. напряжение внутреннего трения пропорционального градиенту скорости.
Коэффициент пропорциональности µ (мю) называется динамическим коэффициентом вязкости. Из формулы видно, что динамический коэффициент вязкости численно равен напряжению внутреннего трения в том случае, когда относительная скорость двух плоскостей А и Б, отстоящих друг от друга на расстоянии 1 м, равна 1м/с.
Размерность динамического коэффициента вязкости следует из формулы. Так как напряжение τ есть сила, отнесенная к единице площади, то его размерность равна:
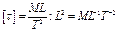 .
.
Размерность градиента скорости:
 .
.
Отсюда размерность динамического коэффициента вязкости:
 .
.
Таким образом, за единицу измерения динамической вязкости в системе единиц СИ принимают:
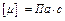 .
.
В физической системе единицей динамической вязкости является пуаз, обозначается «П»:
 .
.
Динамическая вязкость у капельных жидкостей, молекулы которых расположены весьма близко друг к другу, при повышении температуры уменьшается в связи с увеличением скорости броуновского движения, ослабляющего удерживающие связи, то есть силы сцепления.
Зависимость коэффициента μ от температуры в общем виде выражается формулой:
 ,
,
где  - значение
- значение  при t = 0°C; а и b - опытные коэффициенты, зависящие от физико-химических свойств (от рода) жидкости; t - температура жидкости в °С.
при t = 0°C; а и b - опытные коэффициенты, зависящие от физико-химических свойств (от рода) жидкости; t - температура жидкости в °С.
У газов силы притяжения между молекулами проявляют себя только при сильном сжатии, а в обычных условиях молекулы газов находятся в состоянии хаотичного теплового движения и трение слоев газа друг о друга происходит только вследствие столкновения молекул. При повышении температуры скорость молекул возрастает, растет число их столкновений и вязкость возрастает.
Для пресной воды Пуазейлем получена формула:
 . (1.3)
. (1.3)
Для воздуха известна формула Милликена:
 . (1.4)
. (1.4)
В гидравлике для характеристики вязких свойств газов и паров иногда вместо динамического употребляется другой коэффициент вязкости, обозначаемый буквой η (эта) и связанный с динамическим коэффициентом уравнением
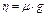 , (1.5)
, (1.5)
где g – ускорение силы тяжести, м/с2.
Очевидно, этот коэффициент вязкости η имеет размерность:
 .
.
При этом единицей измерения η в технической системе единиц является
 .
.
В гидравлике и на производстве широко применяется так называемый кинематический коэффициент вязкости ν (ню), определяемый как отношение динамической вязкости к плотности:
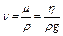 .
.
Размерность кинематического коэффициента вязкости:
 .
.
В системе СИ для ν принята единица:  .
.
Единицей измерения коэффициента ν в физической системе служит стокс, обозначается «Ст»:
 .
.
Например, кинематический коэффициент вязкости воды равен
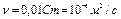 .
.
Величину, обратную динамической вязкости  называют текучестью.
называют текучестью.
Вязкость для всех капельных жидкостей убывает с повышением температуры. Для получения точных гидравлических расчетов рекомендуется иметь график (или таблицу) зависимости вязкости от температуры, построенный на основе специальных определений в лаборатории. Весьма осторожно следует относиться к различного рода номограммам и формулам, служащим для определения вязкости смеси двух или нескольких различных нефтепродуктов.
График, характеризующий зависимость изменения вязкости жидкости от температуры называется вискограммой (Рис. 1.3).

Рис.1.3. Вискограмма
Для определения вязкости жидкости при любой произвольной температуре T с достаточной точностью используется формула Рейнольдса-Филонова:
 ,
,
где ν - вязкость при известной температуре Т, u – коэффициент крутизны вискограммы, который характеризует угол наклона касательной вискограммы к оси абсцисс (Рис. 1.4) и определяется по формуле:
 .
.

Рис.1.4 Определение коэффициента крутизны вискограммы
Таким образом, можно охарактеризовать любую жидкость и определить ее вязкость при любой температуре, зная координаты двух произвольных точек вискограммы. Стоит заметить, что для капельных жидкостей коэффициент вискограммы положителен, однако существуют жидкости, у которых вязкость мало изменяется при изменении температуры, для газообразных - коэффициент вискограммы отрицателен. Существуют жидкости, вязкость которых мало зависит от температуры, они представляют собой сложные химические соединения и используются в качестве рабочих в гидравлических машинах, например в вискомуфтах.
Существуют жидкости, для которых закон И. Ньютона неприменим. В отличие от обычных, ньютоновских, эти жидкости называют неньютоновскими, или аномальными.
Значения кинематической вязкости ν воды и воздуха
| t,0C | 106 ν, м2/c | |
| воды | воздуха | |
| 1,78 | 13,7 | |
| 1,31 | 14,7 | |
| 1,01 | 15,7 | |
| 0,81 | 16,6 | |
| 0,66 | 17,6 | |
| 0,48 | 19,6 | |
| 0,28 | 23,8 |
Таблица 1.6
Кинематическая вязкость некоторых жидкостей
| Жидкость | t, °C | v∙10-4, м2/с | Жидкость | t, °C | v∙10-4, м2/с |
| Бензин | 0,0065 | Ртуть | 0,00125 | ||
| Спирт винный | 0,0133 | Сталь жидкая (0,3% С) | 0,00370 | ||
| Керосин | 0,0250 | ||||
| Глицерин | 8,7000 |
Вязкость различных сортов жидкости одного названия, например, нефти, в зависимости от химического состава и молекулярного строения может иметь различные значения.
Для вязких нефтей средние значения u = 0,05+0,1 на 1°С.
Вязкость жидкостей, как показывают опыты, зависит также от давления. При возрастании давления она обычно увеличивается. Исключением является вода, для которой при температуре до 32° С с повышением давления вязкость уменьшается. При давлениях, встречающихся в практике (до 20 МПа), изменение вязкости жидкостей весьма мало и при обычных гидравлических расчетах не учитывается.
Дата добавления: 2015-04-18; просмотров: 1025; Мы поможем в написании вашей работы!; Нарушение авторских прав |