
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Физические свойства газов
Многие свойства газообразных веществ объясняются кинетической теорией газов, основные положения которой впервые были высказаны М. В. Ломоносовым (рис).
Молекулы газообразного вещества отдалены одна от другой на большие расстояния, в результате чего силы, действующие между ними, очень малы. Размеры молекул ничтожны по сравнению с расстоянием между ними. Вследствие этого газы способны легко сжиматься, значительно уменьшая при этом, свой объем.
Если взять кислород при нормальных условиях и подвергать сжатию, то объем его можно уменьшить в 200 и более раз.
Молекулы газов находятся в непрерывном движении и движутся по прямым линиям во всевозможных направлениях. Явление диффузии, т. е. проникновение молекул одного газа в молекулы другого при их непосредственном соприкосновении, а также свойство газов занимать возможно больший объем находят объяснение в движении молекул газов. Если тот или иной газ заключен в какой-нибудь сосуд, то молекулы его, постоянно ударяясь при движении о стенки сосуда, создают то, что мы называем давлением газа.
При нагревании газа скорость движения молекул увеличивается, сила ударов их о стенки сосуда становится больше, и давление газа возрастает.
Беспорядочное движение молекул можно выразить суммой трех движений в направлении осей х, у и z декартовых координат.
Для понимания основных уравнений кинетической теории газов мысленно выделим кубик газа со стороной а. Пусть скорость молекулы этого газа равна υ, а ее масса т. При расстоянии между противоположными стенками воображаемого кубика, равном а, и пути, проходимому молекулой в 1 с, ω число ударов этой молекулы о стенку будет равно 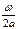 раз в 1 сек. Если считать молекулу абсолютно упругим телом, то следует полагать, что она отскочит от стенки со скоростью, равной по величине и противоположной по направлению первоначальной скорости. Вследствие этого, стенка при каждом ударе приобретает импульс 2 mω, а при
раз в 1 сек. Если считать молекулу абсолютно упругим телом, то следует полагать, что она отскочит от стенки со скоростью, равной по величине и противоположной по направлению первоначальной скорости. Вследствие этого, стенка при каждом ударе приобретает импульс 2 mω, а при  ударах
ударах  . Будем считать, что в воображаемом кубике заключено п молекул. Вдоль каждого ребра кубика будет двигаться 1/3п молекул. Вследствие этого импульс, получаемый каждой стенкой за 1 сек, будет численно равен силе, действующей на всю поверхность стенки, равную a2, т. е.
. Будем считать, что в воображаемом кубике заключено п молекул. Вдоль каждого ребра кубика будет двигаться 1/3п молекул. Вследствие этого импульс, получаемый каждой стенкой за 1 сек, будет численно равен силе, действующей на всю поверхность стенки, равную a2, т. е.  *
* 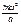 = f.
= f.
Давление, т. е. сила, действующая на единицу поверхности стенки, будет равно
 .
.
В связи с тем, что а3 представляет собой объем кубика или объем газа V, после преобразования получим основное уравнение кинетической теории газов
 . (1.8)
. (1.8)
Так как п молекул массой т имеет общую массу М и находится в объеме V, то из предыдущего уравнения можно написать:
pV =  или Р =
или Р = 
и
 .
.
Отношение M/V есть плотность газа, поэтому при заданном давлении и постоянной температуре скорости молекул обратно пропорциональны корням квадратным из плотностей газов, т.е.
 .
.
Один из основных выводов кинетической теории формулируется следующим образом: молекулы всех газов при одной и той же температуре обладают одинаковой средней кинетической энергией.
Следовательно, с изменением массы молекулы газа скорость ее изменяется так, что произведение массы на квадрат скорости остается постоянным. Тогда давление газа при данной температуре зависит только от числа молекул в единице объема газа, но не зависит от массы молекул, т.е. от природы газа. Отсюда, средние скорости обратно пропорциональны корням квадратным из молекулярных масс, т.е.
 .
.
Кинетическая теория газов позволяет, используя приведенные выше уравнения, вычислить средние скорости движения молекул. Она же лежит в основе объяснений физических свойств газов и законов газового состояния.
Большинство законов газового состояния справедливы для так называемых идеальных газов, т. е. газы, молекулярные силы которых равны нулю, а объем самих молекул бесконечно мал по сравнению с объемом межмолекулярного пространства.
Многие реальные газы близки к идеальным, и поэтому законы газового состояния достаточно объективно отражают их свойства и поведение при изменении внешних условий.
Для идеальных газов справедлив ряд соотношений между их давлением, объемом и температурой, выражаемых законами газового состояния.
Закон Бойля-Мариотта
Английский ученый Роберт Бойль (1627—1691) в 1662 г. и независимо от него французский физик Эдм Мариотт (1620-1684) в 1676 г. установили, что при постоянной температуре объем данной массы газа обратно пропорционален давлению.
Если обозначить объемы, занимаемые газом, через Vо и V, а соответствующие давления через Ро и Р, то в соответствии с основным уравнением (1.8) кинетической теории газов можно написать
 .
.
Так как молекулы всех газов при одной и той же температуре обладают одинаковой средней кинетической энергией, то закон Бойля - Мариотта можно записать следующим образом:

или
 .
.
т.е. при постоянной температуре произведение давления газа на его объем есть величина постоянная.
Плотность газа есть отношение его массы к занимаемому объему:
 .
.
Так как удельные объемы газа υ равны обратной величине плотностей ρ то можно записать:
 .
.
или
 .
.
Если выразить концентрацию газа как весовое его количество в единице объема, то при постоянной температуре давление газа прямо пропорционально его концентрации.
Закон Гей-Люссака
Известный французский химик – Жозеф Луи Гей-Люссак (1778—1850) в 1802 г. установил зависимость между температурой газа и его давлением или объемом.
Из основного уравнения кинетической теории газов (1.8) можно записать:
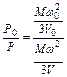 и
и 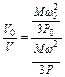 .
.
При постоянном объеме газа первое уравнение примет вид:
 ,
,
а при постоянном давлении второе уравнение можно записать:
 .
.
Так как средняя кинетическая энергия газов является функцией абсолютной температуры, то приведенные выше соотношения могут быть выражены через температуру:
 и
и  (1.9)
(1.9)
или
 и
и 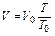 .
.
Таким образом, согласно закону Гей-Люссака, при постоянном объеме давления газов относятся как абсолютные температуры, или при постоянном давлении объемы газов относятся как абсолютные температуры.
Многочисленные опыты показывают, что идеальные газы при нагревании их на 1° при постоянном давлении увеличивают свой объем на постоянную величину, равную  первоначального их объема. Эту величину называют термическим коэффициентом расширения газа и обозначают греческой буквой β =
первоначального их объема. Эту величину называют термическим коэффициентом расширения газа и обозначают греческой буквой β =  .
.
Закон Гей-Люссака может быть сформулирован следующим образом: объем данной массы газа при постоянном давлении есть линейная функция температуры
 , или
, или  .
.
Так как, согласно закону Бойля-Мариотта, PV =const, то при нагревании идеального газа на 10 при постоянном объеме давление его увеличивается на постоянную величину, равную  первоначального давления. Эту величину называли термическим коэффициентом повышения давления газа. Отсюда, согласно закону Гей-Люссака, давление данной массы газа при постоянном объеме есть линейная функция температуры, т.е.
первоначального давления. Эту величину называли термическим коэффициентом повышения давления газа. Отсюда, согласно закону Гей-Люссака, давление данной массы газа при постоянном объеме есть линейная функция температуры, т.е.
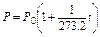 или
или  .
.
Согласно закону Гей-Люссака и основному уравнению кинетической теории газов (1.8) в случае постоянного объема можно записать:

или
 ,
,
или
 .(1.10)
.(1.10)
Таким образом, отношение абсолютных температур газов пропорционально отношению квадратов скоростей их молекул.
Дата добавления: 2015-04-18; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |