
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Закон Паскаля
Основной задачей гидростатики является изучение законов распределения истинных давлений в покоящейся жидкости, а также вычисление их суммарного эффекта при воздействии жидкости на погруженные тела, а также на стенки сосудов.
Теорема: величина истинного гидростатического давления в каждой точке покоящейся жидкости не зависит от расположения плоской площадки, проходящей через эту точку и включающей ее в себя.
Пусть внутри покоящейся жидкости нами рассматривается истинное давление в точке а (рис.2.5 а, стр. 64).

а) б)
Рис. 2.5. Давление в точке а.
Через эту точку можно провести бесчисленное множество плоскостей и в каждой из них построить элемент, включающий в себя точку а. Тогда величина истинного давления может быть определена, с одной стороны, как
 ,
,
с другой стороны, как
 .
.
Необходимо доказать, что независимо от расположения плоскостей:
 .
.
Для доказательства этой теоремы выделим внутри покоящейся жидкости тетраэдр (рис.2.5 б). Построение тетраэдра выполним следующим, образом. Пусть О - точка, относительно которой мы будем доказывать теорему. У точки О как у начала построим прямоугольную систему координат OXYZ.
На осях отложим отрезки Оа, Оb, Оc и через точки а, b, с проведем плоскость, секущую координатный трехгранник. Таким образом, около точки О построен тетраэдр Оаbс. Внутри тетраэдра так же, как и снаружи его, находится покоящаяся жидкость. Допустим, что жидкость внутри тетраэдра затвердела (не меняя при этом своего удельного веса). Равновесное состояние в жидкости при этом не нарушится. Однако это допущение позволяет рассматривать тетраэдр как погруженное тело и вычислять давления, которые оказывает на него окружающая со всех сторон жидкость.
Обозначим силы давления на грани тетраэдра: Рх, Ру, Pz и Рn. При этом сила Рx представляет собой суммарный эффект давления жидкости на грань bОс и, будучи ей перпендикулярна, направлена параллельно оси ох. Точно так же сила Ру, результирующая давления жидкости на грань aOc, будет перпендикулярна этой грани и параллельна оси ОY. Сила Рz аналогично выражает действие жидкости на грань аOb и параллельна оси OZ. Сила Рn выражает суммарное давление на наклонную грань аbс и параллельна направлению внутренней нормали к плоскости этой грани NO.
Обозначим, кроме того, через  средние гидростатические давления на соответствующие грани тетраэдра, а именно;
средние гидростатические давления на соответствующие грани тетраэдра, а именно;
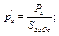

 ,
, 
тогда
 (2.9)
(2.9)
Несомненно, что силы Рx, Рy, Рz и Рn пропорциональны размерам поверхности тетраэдра, т. е. величинам L2.
На рассматриваемый тетраэдр действует, кроме этих четырех поверхностных сил, еще одна объемная сила - сила тяжести. Она будет пропорциональна объему тетраэдра, т. е. величинам L3.
При переходе к пределу, т.е. при безграничном уменьшении размеров тетраэдра, поверхностные силы будут величинами второго порядка малости, в то время как сила тяжести будет величиной третьего порядка малости. Имея это в виду, мы исключаем эту силу из рассмотрения, и равновесие тетраэдра рассматриваем под действием лишь четырех поверхностных сил.
Из статики твердого тела известно, что если тело находится в равновесии, то алгебраическая сумма проекций всех действующих на него сил на любую координатную ось равна нулю. Для пространственной системы сил таких уравнений можно написать три. Спроектируем силы, действующие на тетраэдр, на три оси координат и каждую такую сумму приравняем нулю:
 (2.10)
(2.10)
Принимая во внимание соотношения (1), напишем
 (2.11)
(2.11)
В то же время известно, что проекция любой плоской фигуры на другую плоскость равна площади проектируемой фигуры, умноженной на косинус угла, образуемого перпендикулярами к этим двум плоскостям; следовательно:

Имея это в виду, уравнения (2.11) после сокращений можно написать следующим образом:
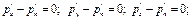
откуда
 (2.12)
(2.12)
Это уравнение тем более справедливо, чем меньше размеры тетраэдра (так как тем законнее исключать из рассмотрения объемную силу - вес тетраэдра). Поэтому выражение
pх = pу = pz = pn, (2.13)
связывающее истинные гидростатические давления в точке О по четырем произвольным направлениям, является вполне точным - теорема доказана.
На основе доказанной теоремы можно установить законы распределения давлений внутри покоящейся жидкости.
Докажем, что если жидкость находится в равновесии и испытывает только действие силы тяжести, то давление изменяется только с глубиной. Во всех точках жидкости, лежащих в одной и той же горизонтальной плоскости, давления будут одинаковы.
Для доказательства этих положений выделим внутри покоящейся жидкости прямоугольный параллелепипед (рис. 2.5, стр. 64). Оси координат расположим так, чтобы плоскость XOY совпадала с какой-нибудь горизонтальной плоскостью, а ось OZ была направлена по вертикали вверх. Ребра параллелепипеда пусть будут параллельны осям координат.
Подобно предыдущему допустим, что жидкость, находящаяся внутри параллелепипеда, затвердела (не изменяя своего удельного веса). При этом равновесие внутри жидкости не нарушится.
Рассматриваемый параллелепипед находится под действием следующих сил:
а) сил поверхностных, находящихся в прямой зависимости от давлений, оказываемы на параллелепипед окружающей его со всех сторон жидкостью; таких сил будет шесть (по числу граней параллелепипеда);
б) силы объемной – силы тяжести.
Так как силы, образующие данную пространственную систему, проходят через одну точку, для их равновесия достаточно написать три уравнения статики твердого тела. Проектируя все силы на три оси координат, получим
 (2.14)
(2.14)
Из первых двух уравнений следует, что силы  , а также
, а также  . Принимая во внимание также равенство площадей противоположных граней параллелепипеда, мы найдем также, что
. Принимая во внимание также равенство площадей противоположных граней параллелепипеда, мы найдем также, что  , а это значит, что средние гидростатические давления на противоположных (вертикальных) гранях одинаковы и не зависят от расстояния между этими гранями. Таким образом, ни в направлении оси ОХ, ни в направлении оси ОY среднее (а тем самым и истинное) гидростатическое давление не меняется: давление во всех точках, лежащих в одной горизонтальной плоскости (плоскости, параллельной осям X и Y), одинаково.
, а это значит, что средние гидростатические давления на противоположных (вертикальных) гранях одинаковы и не зависят от расстояния между этими гранями. Таким образом, ни в направлении оси ОХ, ни в направлении оси ОY среднее (а тем самым и истинное) гидростатическое давление не меняется: давление во всех точках, лежащих в одной горизонтальной плоскости (плоскости, параллельной осям X и Y), одинаково.
Третье из уравнений (2.14) преобразуем, пользуясь следующими соотношениями:

Здесь первые два уравнения выражают силы через соответственные средние гидростатические давления, а последнее - вес через объем параллелепипеда и удельный вес жидкости. Тогда
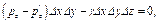
откуда после сокращений получим:
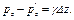 (7)
(7)
Из этого соотношения видно, что средние гидростатические давления на двух горизонтальных гранях параллелепипеда не одинаковы. Несомненно, что если расстояние между этими гранями Δz мало, то мало будут различаться между собой и эти давления. Итак, пусть

Тогда
 (2.15)
(2.15)
Это уравнение известно под названием основного уравнения гидростатики.
Так как для капельных жидкостей γ=const и если известно давление в какой-либо определенной точке покоящейся жидкости, то с помощью уравнения (2.15) можно найти давление и во всякой другой точке.

Рис.2.6. Распределение давления в покоящейся жидкости
Допустим, что в точке О (рис.2.6), имеющей вертикальную координату zo. давление равно pо, тогда в точке М, координата которой равна z, давление р определится из уравнения

здесь


Это уравнение можно представить и в следующем, наиболее часто встречающемся, виде:
 ,
,
 . (2.16)
. (2.16)
Из уравнения (2.16) следует, что избыточное давление на дно сосуда зависит только от высоты столба жидкости. Так, например, во всех сосудах, представленных на рисунке, давление на дно сосуда одинаково. Это явление называется гидростатическим парадоксом (рис. 2.7).

Рис.2.7. Гидростатический парадокс
Из этого же соотношения следует, что если в точке О давление увеличится на какую бы то ни было величину, то на такую же величину возрастет давление и во всякой другой точке М. В этом заключается закон Паскаля.
Вертикальные координаты zo и z, отсчитанные вверх от одной и той же
условной горизонтальной плоскости представляют собой нивелирные высоты. Как известно, при помощи геодезического инструмента - нивелира - измеряют относительные высоты различных объектов, отсчитывая их от одной и той же условной горизонтальной плоскости.
Так как вывод формулы (2.16) не ставится нигде в зависимость от формы сосуда, то очевидно, что закон Паскаля будет справедлив для любого случая абсолютного покоя однородной тяжелой несжимаемой жидкости.
Основное уравнение гидростатики  показывает, что давление на поверхности жидкости p0 передается в любую точку внутри жидкости без изменения.
показывает, что давление на поверхности жидкости p0 передается в любую точку внутри жидкости без изменения.
В связи с этим, учитывая второе свойство гидростатического давления, можно сформулировать закон Паскаля: давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково.
Дата добавления: 2015-04-18; просмотров: 252; Мы поможем в написании вашей работы!; Нарушение авторских прав |