Давление на плоскую стенку

Задача определения суммарного давления жидкости на стенку представляет большое практическое значение при расчете резервуаров, емкостей, плотин, подпорных стенок и т.д.

Наиболее просто эта задача решается для случая давления жидкости на плоскую наклонную стенку. Задача об определении суммарного давления жидкости ставиться заключается в отыскании силы полного избыточного давления, т.е. нахождения ее величины, направления и точки приложения.

Пусть необходимо определить силу полного давления на плоскую стенку, наклоненную под углом α к горизонту (рис.2.22). Величина смоченной поверхности стенки пусть равна F, а глубина центра тяжести смоченной поверхности, отсчитанная от свободного уровня, z_ц.т.

Рис.2.22. Плоская наклонная стенка

В общем виде эта задача решается следующим образом.

Так как стенка представляет собой плоскость, то давления на все отдельные элементы будут перпендикулярны плоскости стенки и, следовательно, параллельны между собой. Таким образом, задача отыскания силы суммарного давления сводиться к определению равнодействующей системы параллельных сил, одинаково направленных.

Совместим плоскость отсчета высот со свободной поверхностью, тогда все глубины будут отсчитываться в отрицательном направлении оси Оz.

Выберем две точки: одну на поверхности уровня z₀=0 и , а другую на стенке, на глубине – z. Избыточное давление в этой точке на основании уравнения (2.19) определиться из соотношения

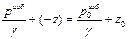
которое на основании выбранных условий дает

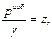
или

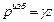(2.30)

Из этого уравнения видно, что давление в жидкости растет прямо пропорционально первой степени глубины. Закон изменения давле­ния представлен на рис. 2.23 в виде прямой линии.

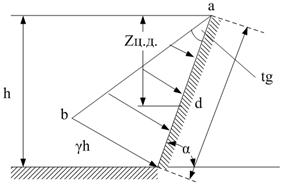
Рис.2.23. Закон изменения давления по высоте плоской стенки

Здесь тангенс угла при вершине в известном масштабе представляет собой γ (удельный вес). Итак, гидростатические давления на плоскую стенку могут быть изображены как система параллельных сил, равномерно возрастающих с глубиной (рис. 2.24, стр. 87). Такая расчетная схема сводит задачу к определению некоторой неравномерно распределенной нагрузки на плоскость стенки. Величина этой нагрузки будет равна объему фигуры, образованной плоскостью стенки, плоскостью, составляющей со стенкой угол, тангенс которого равен γ, и цилиндрической поверхностью, образующие которой пер­пендикулярны к плоскости стенки и проходят через контур стенки.

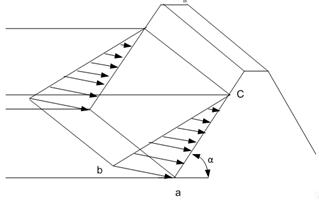
Рис.2.24. Давления жидкости на плоскую стенку

Следовательно, полная сила давления жидкости на плоскую стенку равна про­изведению площади стенки S на гидростатическое давление p в центре тяжести этой площади:

.

Если бы все точки рассматриваемой стенки испытывали оди­наковое давление со стороны жидкости, то сила давления на всю стенку была бы равна произведению площади S на гидростатическое давление в любой из точек стенки, как в случае давления на дно сосуда.

Таким образом, можно вычислить величину силы полного давле­ния. Направление ее будет, так же как направление составляющих сил, перпендикулярно стенке, а точка приложения силы полного давления, называемая центром давления, будет совпадать с центром тяжести фигуры, изображающей собой нагрузку на стенку.

Рассмотрим частный случай давления на плоскую прямоугольную стенку, наклоненную к горизонту под углом α (рис. 2.25, стр. 88). Глубина около нижнего основания стенки пусть равна h, а ширина стенки b. В этом случае длина наклонной стенки будет равна

.

Давление на такую стенку представится в виде нагрузки в форме треугольной призмы. В основании эта призма имеет прямоугольный треугольник АВС с катетами АС = х и АВ = γh, при этом АВ – давление у нижнего основания стенки.

Объем этой фигуры будет равен

а, следовательно, полное давление

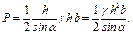
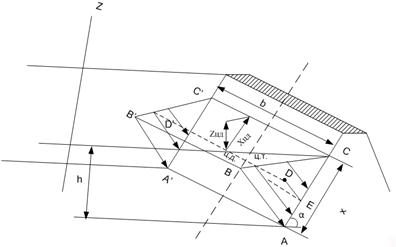
Рис.2.25. Призма давлений

Центр тяжести прямоугольной призмы будет расположен на середине горизонтальной линии DD', проходящей через центры тяжести треугольников АВС и А'В'С'.

Для треугольника, как известно, положение центра тяжести определяется точкой пересечения медиан. Эта точка находится на расстоянии от стороны АВ, равном 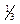высоты треугольника АВС, т. е. в точке D. Тогда 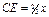, а координата центра давления z_{ц. д.} равна:

Таким образом, центр давления для плоской прямоугольной стенки расположен на глубине, равной 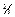глубины, около нижнего основания стенки.

Так как фигура, представляющая собой суммарное давление жидкости на стенку (рис. 2.25), не симметрична относительно горизон­тальной плоскости, а смещена в сторону возрастания глубин, то совершенно очевидно, что центр давления (ц.д.) на всякую плоскую стенку всегда лежит ниже центра тяжести (ц.т.) фигуры, изобра­жающей смоченную часть плоской стенки. Для случая, изображен­ного на рис. 2.25, т. е. для прямоугольной стенки АА'С'С, центр тяжести смоченной фигуры находится на глубине 0,5h.