
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Давление жидкости на криволинейные стенки.
2.8.1. Определение равнодействующей силы давления
в трехмерном измерении
Всякую кривую стенку можно рассматривать как предел, к которому стремится многогранник, вписанный (или описанный) в кривую поверхность стенки, при безграничном уменьшении размеров граней (рис. 2.29). Таким образом, полное давление жидкости на кривую стенку можно найти, суммируя давление на плоские, грани многогранника, вписанного (или описанного) в заданную поверхность, и переходя затем к пределу. Однако так как плоские грани многогранника будут пересекаться между собой под различными углами, то и силы давления, приложенные к этим граням, не будут между собой параллельны. В этом случае сила полного давления не будет равна алгебраической сумме сил составляющих и для определения суммарного давления придется прибегнуть к методу проекций.

Рис. 2.29. Давление на сегмент криволинейной стенки
Из теоретической механики (статики) известно, что проекция равнодействующей системы сил на какую-нибудь ось равна алгебраической сумме проекций сил составляющих на ту же ось. Сила, действующая на грань А, грань весьма малую (размер которой обозначим ΔS), будет тоже величина малая ΔP. Спроектируем эту силу на три оси координат Х, Y и Z. Тогда, обозначив проекции ΔP на оси соответственно ΔPx, ΔPy и ΔPz, напишем:
 (27)
(27)
При этом сила
 .
.
Итак,
 (2.31)
(2.31)
Как известно, площадь проекции какого-либо плоского элемента на какую-нибудь плоскость равна произведению площади этого элемента на косинус угла, образуемого перпендикулярами, проведенными к обеим плоскостям.
Поэтому произведения элемента площади ΔF на соответствующие косинусы будут равны проекциям этой площади на плоскости координатного трехгранника:

В самом деле, ΔP перпендикулярно ΔF, а х - координатной плоскости ZOY.
Точно так же имеем:

и, следовательно,
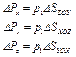 (2.32)
(2.32)
Подобным же образом давление на грань В (рис.2.29) (размеры которой обозначим ΔW), равное Δτ, может быть разложено на три составляющих по осям Х, Y и Z:
 (2.33)
(2.33)
На основании формулы (2.31) можно написать, что избыточные средние гидростатические давления на грани А и В соответственно равны

Теперь остается просуммировать соответственные проекции и определить таким образом проекции Рх, Ру и Рz равнодействующей, т. е. силы Р - полного давления жидкости - на кривую стенку. На основании формул (2.32) и (2.33) напишем:
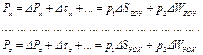 (2.34)
(2.34)
Итак, чтобы найти горизонтальные проекции силы Р, а именно Рx и Ру, следует определить давления на соответствующие проекции граней многогранника на вертикальные плоскости координатного трехгранника и затем их алгебраически сложить. В самом деле, произведение 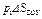 представляет собой давление жидкости на вертикальную плоскую стенку, размер которой равен проекции грани А многогранника на вертикальную плоскость YOZ.
представляет собой давление жидкости на вертикальную плоскую стенку, размер которой равен проекции грани А многогранника на вертикальную плоскость YOZ.
Точно так же  равно давлению жидкости на вертикальный элемент плоскости YOZ, отображающий проекцию элемента многогранника, вписанного в поверхность кривой стенки.
равно давлению жидкости на вертикальный элемент плоскости YOZ, отображающий проекцию элемента многогранника, вписанного в поверхность кривой стенки.
Итак, проекция на какую-либо горизонтальную ось силы полного давления жидкости на кривую стенку равна полному давлению жидкости на фиктивную вертикальную стенку. Величина и форма этой фиктивной стенки равны проекции данной кривой стенки на плоскость, перпендикулярную направлению горизонтальной оси.
Таким образом, проекция Рx равна давлению жидкости на плоскую стенку L, величина которой равна проекции кривой стенки К на плоскость YOZ.
Проекция силы Р на ось Y аналогично представится как сила полного давления жидкости на вертикальную плоскую стенку М, величина которой в точности равна проекции кривой стенки на плоскость XOZ.
Вертикальная проекция силы Р (на ось Z) на основании формул (2.33) и (2.34) равна:
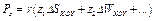 (2.35)
(2.35)
Из рис. нетрудно видеть, что выражения, стоящие в скобках, представляют собой объемы жидкости, расположенные над соответствующими элементами граней многогранника. В самом деле, произведение  соответствует объему столбика, в основании которого лежит элемент многогранника А, а высота равна глубине, на которой лежит этот элемент А (рис. 2.30) под уровнем жидкости.
соответствует объему столбика, в основании которого лежит элемент многогранника А, а высота равна глубине, на которой лежит этот элемент А (рис. 2.30) под уровнем жидкости.

Рис. 2.30. Проецирование фигур
Если произвести суммирование формулы (2.35), то, как нетрудно убедиться, выражение, заключенное в скобки, будет равно объему жидкости, расположенному над всей кривой стенкой, а вертикальная проекция силы полного давления
 (2.36)
(2.36)
окажется равной весу жидкости, взятой в объеме V, расположенном над всей кривой стенкой.
Дата добавления: 2015-04-18; просмотров: 265; Мы поможем в написании вашей работы!; Нарушение авторских прав |