
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диффузионный массообмен
Скорость диффузии частиц типа А в смеси частиц А и В (такой процесс переноса часто называют бинарной диффузией, поскольку в смеси присутствуют только два типа частиц) определяется первым законом диффузии Фика. Этот закон можно записать на основе массовых представлений, когда поток массы измеряется в кг/с, или на основе молярных представлений, когда поток массы измеряется в моль/с.
В 1855 году немецкий физик Адольф Фик сформулировал следующий закон молекулярного переноса массы:
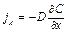 , (3.39)
, (3.39)
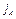 – поток массы частиц типа А, то есть переносимое по оси х количество их массы за 1 с, кг/(м2с);
– поток массы частиц типа А, то есть переносимое по оси х количество их массы за 1 с, кг/(м2с);  – градиент концентрации по оси х или плотность переносимой массы кг/м3; D – коэффициент диффузии, м2/с; х – направление, в котором измеряется поток массы, м; знак "минус" указывает на направление потока от больших концентраций к меньшим.
– градиент концентрации по оси х или плотность переносимой массы кг/м3; D – коэффициент диффузии, м2/с; х – направление, в котором измеряется поток массы, м; знак "минус" указывает на направление потока от больших концентраций к меньшим. Если концентрация вещества измеряется не в кг/м3, а в других единицах, например, относительная концентрация м3/м3 %, объемная м3, то единицы измерения коэффициента диффузии будут иные.
Коэффициент диффузии меняется в очень широких пределах: на десять порядков, от 10-4 до 10-14 м2/с.
Если помимо молекулярного переноса массы существует и конвективный (называемый Стефановским потоком), то общий поток массы описывается обобщенным законом Фика:
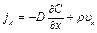 , (3.40)
, (3.40)
где 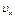 – составляющая скорости в направлении оси x. Первый член правой части уравнения характеризует молекулярный перенос вещества, второй – конвективный перенос, связанный с движением смеси, как целого, со средней скоростью
– составляющая скорости в направлении оси x. Первый член правой части уравнения характеризует молекулярный перенос вещества, второй – конвективный перенос, связанный с движением смеси, как целого, со средней скоростью 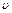 .
.
Первый закон Фика можно выразить также через градиент парциальных давлений.
Около поверхности жидкости образуется паровоздушная смесь, в которой на любом расстоянии от поверхности сумма относительных концентраций компонента пара 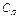 и среды (воздуха)
и среды (воздуха) 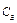 равна единице
равна единице
 (3.41)
(3.41)
Считая диффундирующий компонент (пар) и воздух идеальными газами, выразим их относительные концентрации через парциальные давления и после преобразования уравнения (3.39) получим
 , (3.42)
, (3.42)
где 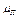 ,
, 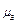 - молярные массы пара и воздуха, р – сумма их парциальных давлений (
- молярные массы пара и воздуха, р – сумма их парциальных давлений ( 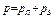 ).
).
В практических расчетах (испарение воды в воздух, испарение топлива в поршневых ДВС) поправкой
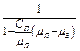
пренебрегают. Тогда уравнение запишется (3.42) как
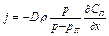 . (3.43)
. (3.43)
Заменив градиент относительных концентраций на градиент парциальных давлений, а также проинтегрировав данное уравнение (3.43), при постоянных массовом потоке и температуре, в пределах х=0, l; 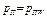 ;
;  получим:
получим:
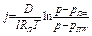 , (3.44)
, (3.44)
где 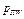 ,
,  - парциальные давления пара у поверхности и на расстоянии l от поверхности;
- парциальные давления пара у поверхности и на расстоянии l от поверхности;  - газовая постоянная паров компонентов.
- газовая постоянная паров компонентов.
Второй закон Фика связывает пространственное и временное изменения концентрации (уравнение диффузии)
 , (3.45)
, (3.45)
Коэффициент диффузии D зависит от температуры. Значения коэффициентов диффузии в жидкой фазе на несколько порядков величины меньше, чем в газовой фазе, поскольку подвижность молекул жидкости намного меньше, чем молекул газа.
Дата добавления: 2015-04-18; просмотров: 247; Мы поможем в написании вашей работы!; Нарушение авторских прав |