
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Установившаяся фильтрация идеального газа
Уравнение состояния идеального газа при изотермическом течении можно записать так
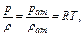 (4.81)
(4.81)
где ρат – плотность газа при атмосферном давлении и пластовой температуре.
Отсюда
 (4.82)
(4.82)
поэтому функция Лейбензона для идеального газа имеет вид
 (4.83)
(4.83)
где р – абсолютное давление.
Параллельно - струйная фильтрация идеального газа по закону Дарси
При параллельно – струйной фильтрации газа формула массового расхода имеет вид:
 (4.84)
(4.84)
или
 (4.85)
(4.85)
Приведенным расход Qат назовём объёмный расход, приведенный к атмосферному давлению и пластовой температуре
 (4.86)
(4.86)
Из формулы (4.84) получим
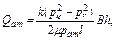 (4.87)
(4.87)
Заменяя в формуле (4.25), выражающей закон распределения давления при параллельно – струйной фильтрации несжимаемой жидкости, р на Р, получим распределение функции Лейбензона по линейному закону
 (4.88)
(4.88)
и, используя формулу распределения давления по параболическому закону
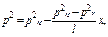 (4.89)
(4.89)
Средневзвешенное по объёму пласта давление газа равно
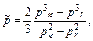 (4.90)
(4.90)
Плоскорадиальная фильтрация газа
В соответствии с формулой Дюпюи получим формулу для массового дебита газа
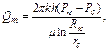 (4.91)
(4.91)
Подставляя значение функции Лейбензона (4.82) в предыдущую формулу, найдём
 (4.92)
(4.92)
а выражение для объёмного дебита газовой скважины, приведенного к атмосферному давлению и пластовой температуре, получим в виде
 (4.93)
(4.93)
Заменяя в формуле (4.29) р на Р, получим логарифмический закон распределения Р :
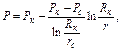 (4.94)
(4.94)
откуда, найдём закон распределения давления
 (4.95)
(4.95)
Средневзвешенное пластовое давление газа при установившейся плоскорадиальной фильтрации по закону Дарси определяется приближение по формуле
 . (4.96)
. (4.96)
Таким образом при плоскорадиальная фильтрация идеального газа при нелинейном законе фильтрации, дебит скважины, приведенный к атмосферному давлению и пластовой температуре, определяется по формуле
 (4.97)
(4.97)
Дата добавления: 2015-04-18; просмотров: 289; Мы поможем в написании вашей работы!; Нарушение авторских прав |