Дифференциальные уравнения Эйлера. Основное уравнение гидростатики в дифференциальной форме

Соотношение между силами, действующими на жидкость, которая находится в состоянии покоя, определяющее условия равновесия жидкости, выражается дифференциальными уравнениями равновесия Эйлера.

В жидкости выделим элементарный объем в виде параллелепипеда с ребрами dx ,dy, dz, расположенными параллельно осям координат х, у и z.

На выделенный параллелепипед действуют массовые и поверхностные силы. В данном случае поверхностные силы – силы давления на грани параллелепипеда.

Рисунок 3 – Элементарный параллелепипед

Рассмотрим условие равновесия выделенного элементарного объема.

Обозначим через X, Y, Z проекции единичных массовых сил на оси координат, представляющих собой проекции ускорений на соответствующие координатные оси. Массовые силы, действующие на выделенный элементарный объем в направлении координатных осей, будут равны произведению ускорений на массу элементарного объема . Например, проекция массовой силы на ось х представляет собой:

Сила гидростатического давления на любую из граней параллелепипеда равна произведению гидростатического давления р на площадь этой грани ( 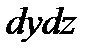). Будем считать, что давление р является функцией всех трех координат:

,

Согласно основному принципу статики, сумма проекций на оси координат всех сил, действующих на элементарный объем, находящийся в равновесии, равна нулю. В противном случае происходило бы перемещение жидкости.

Рассмотрим сумму проекций сил на ось x. Сила гидростатического давления действует на левую грань параллелепипеда по нормали к ней и ее проекция на ось x равна p^.dydz. Изменение гидростатического давления в направлении оси x составляет (градиент давления вдоль оси x). Тогда давление жидкости на правой грани будет равно и сила давления на правую грань равна .

Сумма проекций сил на ось x равна нулю, т.е.

После сокращений получаем:

,

так как это объем параллелепипеда, тогда:

,

Для трех координатных осей соответственно получим:

Это выражение называется системой дифференциальных уравнений Эйлера для покоящейся жидкости.

Разделив все уравнения на плотность 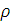и умножив первое уравнение на , второе на и третье на после сложения уравнений, получим:

,

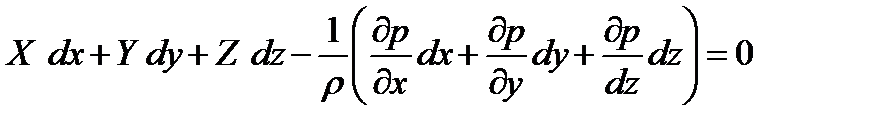т.к. давление является только функцией координат, то выражение есть полный дифференциал – dp.

,

где

Приращение давления при изменении координат согласно уравнения Эйлера составляет:

полученное уравнение является основным уравнением гидростатики в дифференциальной форме [1,2,5].