Подготовка к лабораторной работе. 5.2.1 Изучить материал по теме данной работы в настоящем пособии, а также в рекомендованной литературе ([1]

5.2.1 Изучить материал по теме данной работы в настоящем пособии, а также в рекомендованной литературе ([1], С. 103-107; [2] С. 87-92).

5.2.2 Выучить определения основных понятий и терминов темы (Приложение Б).

Основные термины и понятия:

– автомодельный режим движения;

– внутренняя задача гидродинамики;

– вязкость;

– гидродинамический напор;

– гладкое течение;

– зона стабилизации;

– коэффициент гидравлических сопротивлений;

– «потерянный напор».

5.3 Теоретические сведения

Гидравлические потери на трение – потери при движении жидкости в прямых каналах, трубах (рисунок 5.1), поперечное сечение которых постоянно по форме и площади. Потери на трение обусловлены вязкостным трением слоев жидкости, движущихся внутри потока с разной скоростью, а также трением о внутреннюю поверхность трубы слоев жидкости, движущихся в непосредственной близости от нее. Однако величина потерь на трение определяется не только вязкостью жидкости, но и зависит от скорости её движения, от площади внутренней поверхности канала и её шероховатости. Площадь поверхности канала, как известно, зависит от его длины и формы поперечного сечения.

Рисунок 5.1 – Гидравлические потери на трение

В расчетах величина потерь на трение подсчитывается по формуле:

, (5.1)

где λ – коэффициент гидравлических потерь на трение (по длине);

l – длина прямого участка трубы, м;

d_э – эквивалентный диаметр канала, м.

Коэффициент гидравлических потерь λ является мерой отношения скоростного напора и величины потерь на трение на участке (см. рисунок 5.1) длиной, равной эквивалентному диаметру канала, то есть когда l = d_э. При ламинарном режиме движения коэффициент λ зависит только от числа Рейнольдса:

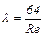. (5.2)

При турбулентном режиме движения коэффициент λ зависит как от числа Рейнольдса, так и от относительной шероховатости поверхности стенок канала. При этом существуют три области гидравлического трения:

– область гидравлически гладких труб, где λ = f(Re);

– область доквадратичного сопротивления, где λ = f(Re, Δ/d);

– область квадратичного сопротивления, где λ = f(Δ/d).

Механизм гидравлического трения в каждой из этих областей зависит от соотношения размеров ламинарного подслоя толщиной δ и размеров шероховатости внутренней поверхности канала Δ (рисунок 5.2).

Рисунок 5.2 – Схема гидравлического трения при турбулентном

режиме движения жидкости

В области гидравлически гладких труб δ > Δ, поэтому вязкий подслой покрывает выступы шероховатости, и турбулентное ядро потока не взаимодействует с шероховатостью.

В области доквадратичного сопротивления (δ ≈ Δ) происходит постепенное ''раскрывание'' шероховатости турбулентным ядром. Здесь имеет место общий случай зависимости λ = f(Re, Δ/d).

И, наконец, в области квадратичного сопротивления, когда выступы полностью ''раскрыты'', значение λ зависит только от размеров шероховатости.

На практике при расчете технических труб границы областей гидравлического трения определяют в зависимости от предельных чисел Рейнольдса:

, (5.3)

, (5.4)

где – относительная эквивалентная шероховатость;

Δ_э – эквивалентная шероховатость, характеризующая среднюю высоту выступов технических труб.

Если Re_кр < Re < Re_пр^I, имеем область гидравлически гладких труб. Для расчета коэффициента гидравлического трения рекомендуется формула:

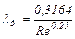. (5.5)

Если Re_пр^I < Re <Re_пр^II, имеем область доквадратичного сопротивления. Для расчета λ рекомендуется формула:

. (5.6)

Если Re > Re_пр^II, имеем область квадратичного сопротивления. Рекомендуется формула:

. (5.7)

Для всех областей и режимов движения жидкости в трубах с естественной шероховатостью коэффициент гидравлического трения можно определить с помощью графика Кольбрука-Мурина [2].

При установившемся движении жидкости в горизонтальных каналах с постоянным по форме и размерам поперечным сечением средняя скорость потока и, следовательно, скоростной напор одинаковы во всех сечениях. Поэтому уравнение Бернулли (1.8) принимает вид:

,

откуда . (5.8)

Таким образом, гидравлические потери на трение можно измерить непосредственно (см. рисунок 5.1) как разность Δh высот уровней h₁ и h₂ жидкости в пьезометрах, установленных в начале и в конце рассматриваемого участка длиной l.