
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определяемые параметры
Исходные данные
Таблица 2.1.
| Вариант 2 | Вариант 14 | Вариант 26 | |||
| Величина | Значение | Величина | Значение | Величина | Значение |
| Н1, м | 4,20 | r1, кг/м3 | Q, л/с | ||
| Н3, м | 0,8 | n1, см2/с | 0,13 | r1, кг/м3 | |
| l1, м | l1, м | n1, см2/с | 0,13 | ||
| l2, м | l2, м | l1, м | |||
| l3, м | l3, м | l2, м | |||
| l4, м | l4, м | l3, м | |||
| l5, м | l5, м | l4, м | |||
| l6, м | l6, м | l5, м | |||
| l7, м | l7, м | l6, м | |||
| l8, м | l8, м | l7, м | |||
| l9, м | l9, м | l8, м | |||
| l10, м | l10, м | l9, м | |||
| lc, м | lc, м | l10, м | |||
| lэкв., м | lэкв., м | lc, м | |||
| d1, мм | d1, мм | lэкв., м | |||
| d2, мм | d2, мм | d1, мм | |||
| dвен, мм | D, мм | 0,66 | d2, мм | ||
| dнас, мм | Dс, мм | 0,6 | D, мм | 0,6 | |
| D, мм | 0,15 | Н3, мм | 3,5 | Dс, мм | 0,6 |
| Dс, мм | 0,3 | xкор | Н3, мм | 3,5 | |
| xкор | xкол | 1,5 | xкор | ||
| xкол | 1,2 | xзад | 2,0 | xкол | 1,5 |
| xзад | dвен, мм | xзад | |||
| r1, кг/м3 | mвен | 0,92 | РВ, кПа | ||
| n1, см2/с | 0,01 | hвен, мм рт.ст | РМ1, кПа | ||
| r2, кг/м3 | r2, кг/м3 | dвен, мм | |||
| mнас | 0,8 | РВ, кПа | mвен | 0,92 | |
| mвен | 0,97 | РМ1, кПа | r2, кг/м3 | ||
| РВ, кПа | dнас, мм | dнас, мм | |||
| РМ1, кПа | mнас | 0,95 | mнас | 0,95 |
Описание установки
Жидкость по самотечному трубопроводу поступает из верхнего резервуара А в нижний резервуар В, откуда насосом перекачивается в промежуточную ёмкость С и из неё выливается в резервуар А.
На всасывающей линии насосной установки имеется всасывающая коробка с обратным клапаном 1, поворотное колено 2, задвижка 3, вакуумметр РВ.
На нагнетательной линии установлены манометры РМ1, РМ2, РМ3, скоростная трубка 5 расходомер Вентури 6. Промежуточная ёмкость С в донной части имеет насадок 7.
Определяемые параметры
1) Определить геометрическую высоту всасывания насоса Н2.
2) Определить показание дифманометра (или дифпьезометра) скоростной трубки.
3) Построить эпюру скоростей для сечения в месте установки скоростной трубки.
4) Определить показание дифманометра расходомера Вентури (hвен).
5) Определить разность показаний манометров Рм2 и Рм3.
6) Определить суммарные потери напора в местных сопротивлениях нагнетательной линии и их суммарную эквивалентную длину.
7) Определить необходимый диаметр самотечного трубопровода dc, обеспечивающий установление заданного постоянного уровня в верхнем резервуаре Н3.
8) Определить минимальную толщину стальных стенок трубы d2, при которой не происходит её разрыва в момент возникновения прямого гидравлического удара.
9) Определить полезную мощность насоса.
2.4. Определение геометрической высоты всасывания насоса Н2.
Вариант 2
2.4.1Для определения геометрической высоты всасывания насоса Н2 рассмотрим два сечения А-А (поверхность жидкости в нижнем резервуаре В) и В-В (в месте установки вакуумметра Рв во всасывающей линии насосной установки). Мы имеем дело с установившимся движением вязкой несжимаемой жидкостью. Запишем уравнение Бернулли для сечения А-А и В-В:
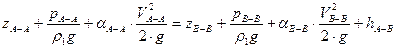 …(1)
…(1)
где  ,
,  - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
- расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
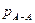 ,
,  - давления в сечениях А-А и В-В соответственно (Па);
- давления в сечениях А-А и В-В соответственно (Па);
 - плотность циркулирующей жидкости (кг/м3);
- плотность циркулирующей жидкости (кг/м3);
g - ускорение свободного падения (м2/с);
VA-A ,VB-B - скорость течения жидкости в сечение А-А и В-В соответственно (м/с);
 ,
, 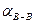 - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
- коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
 - потери напора на участках между выбранными сечениями.
- потери напора на участках между выбранными сечениями.
Выберем сечение А-А за начало отсчёта, тогда zА-А=0 и zВ-В=Н2.
VA-A=0, так как уровень в нижнем резервуаре В установившийся.
 , так как резервуар В открыт.
, так как резервуар В открыт.
 - разность атмосферного и вакуумного давления.
- разность атмосферного и вакуумного давления.
Для решения практических задач коэффициент Кориолиса можно принять равным единице, т.е. 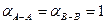 .
.
 , где Q – расход жидкости (м3/с); S- площадь поперечного сечения (м2).
, где Q – расход жидкости (м3/с); S- площадь поперечного сечения (м2).

В результате формула (1) примет вид:
 …(2)
…(2)
Для определения Н2 необходимо определить расход Q и потери напора hA-B.
2.4.2.Расход жидкости можно определить по установившемуся уровню жидкости в промежуточной ёмкости Н1, зная диаметр и коэффициент расхода насадка - dнас, μнас по формуле:
 ;
; 
где  -площадь отверстия насадка (м2); Н0 – приведённый напор, который определяется по формуле
-площадь отверстия насадка (м2); Н0 – приведённый напор, который определяется по формуле  , где
, где  -давления на поверхности промежуточной ёмкости и давление под насадком соответственно. Имеем, что р1=р2=ратм, т.к. ёмкость открыта. Тогда Н0= Н1.
-давления на поверхности промежуточной ёмкости и давление под насадком соответственно. Имеем, что р1=р2=ратм, т.к. ёмкость открыта. Тогда Н0= Н1.
Следовательно, 
2.3.3.Определим потери напора hА-В.
hА-В=hд+hм (3) , где hд - потери напора по длине трубопровода (м); hм- потери напора от местных сопротивлений.
hм= hкор +hкол+hзад , где hкор- потери напора на коробке всасывающей линии (м);
hкол- потери напора на колене всасывающей линии (м);
hзад- потери напора на задвижке всасывающей линии (м).

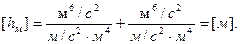
hд=hд1+hд2 , где hд1- потери напора на участке трубопровода l1;
hд2- потери напора на участке трубопровода l2.
 ;
;  ;
; 
где  - коэффициент гидравлического сопротивления для соответствующего участка.
- коэффициент гидравлического сопротивления для соответствующего участка.
Для определения λ1 и λ2 необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Re для этих участков:


где ν- кинематическая вязкость циркуляционной жидкости (м2/с).
Имеем, что Re1>Reкр=2300  на участке трубопровода l1 турбулентный режим течения;
на участке трубопровода l1 турбулентный режим течения;
Re2>Reкр=2300  на участке трубопровода l2 турбулентный режим течения.
на участке трубопровода l2 турбулентный режим течения.
Определим тип трубопровода (шероховатый или гладкий) на участках трубопровода l1 и l2.
Для этого определим значения величин обратной относительной шероховатости для обоих рассматриваемых участков:

Оба участка принадлежат зоне шероховатых труб, т.к. их числа Re принадлежат промежуткам:
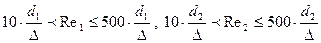
 для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:
для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:

Найдём суммарные потери напора для участков l1 и l2:
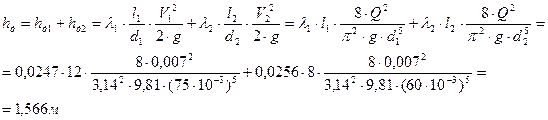

Подставим полученные нами значения в формулу (3) и получим необходимую величину:
hА-В=hд+hм=1,566+1,708=3,274м.
2.4.4.По формуле (2) определим геометрическую высоту всасывания насоса Н2:
 .
.

Вариант 14
2.4.1Для определения геометрической высоты всасывания насоса Н2 рассмотрим два сечения А-А (поверхность жидкости в нижнем резервуаре В) и В-В (в месте установки вакуумметра Рв во всасывающей линии насосной установки). Мы имеем дело с установившимся движением вязкой несжимаемой жидкостью. Запишем уравнение Бернулли для сечения А-А и В-В:
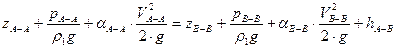 …(1)
…(1)
где  ,
,  - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
- расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
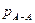 ,
,  - давления в сечениях А-А и В-В соответственно (Па);
- давления в сечениях А-А и В-В соответственно (Па);
 - плотность циркулирующей жидкости (кг/м3);
- плотность циркулирующей жидкости (кг/м3);
g - ускорение свободного падения (м2/с);
VA-A ,VB-B - скорость течения жидкости в сечение А-А и В-В соответственно (м/с);
 ,
, 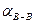 - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
- коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
 - потери напора на участках между выбранными сечениями.
- потери напора на участках между выбранными сечениями.
Выберем сечение А-А за начало отсчёта, тогда zА-А=0 и zВ-В=Н2.
VA-A=0, так как уровень в нижнем резервуаре В установившийся.
 , так как резервуар В открыт.
, так как резервуар В открыт.
 - разность атмосферного и вакуумного давления.
- разность атмосферного и вакуумного давления.
Для решения практических задач коэффициент Кориолиса можно принять равным единице, т.е. 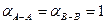 .
.
 , где Q – расход жидкости (м3/с); S- площадь поперечного сечения (м2).
, где Q – расход жидкости (м3/с); S- площадь поперечного сечения (м2).

В результате формула (1) примет вид:
 …(2)
…(2)
Для определения Н2 необходимо определить расход Q и потери напора hA-B.
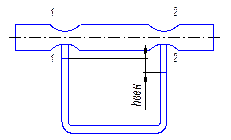 2.4.2.Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури.
2.4.2.Для определения расхода жидкости рассмотрим ртутный дифманометр расходомера Вентури.
Запишем уравнение неразрывности для сечений 1-1 и 2-2:

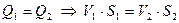 (1)
(1)
Выразим из (1) скорость  :
:
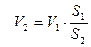 (2).
(2).
Запишем уравнение Бернулли Для двух сечений 1-1 и 2-2:
 (3)
(3)
где  ,
,  - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
- расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);
 ,
,  - давления в сечениях А-А и В-В соответственно (Па);
- давления в сечениях А-А и В-В соответственно (Па);
 - плотность циркулирующей жидкости (кг/м3);
- плотность циркулирующей жидкости (кг/м3);
g - ускорение свободного падения (м2/с);
V1 ,V2 - скорость течения жидкости в сеченьях А-А и В-В соответственно (м/с);
 ,
,  - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
- коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;
 - потери напора на участках между выбранными сечениями.
- потери напора на участках между выбранными сечениями.
Выберем ось трубопровода за начало отсчёта, тогда z1=z2=0, т.к. трубопровод горизонтален. Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора hA-B=0.
α1=α2=1, (для практических расчётов).
Запишем (3) с учётом всех утверждений:
 (4).
(4).
Выразим из (4) с учётом (2):
 (5)
(5)
Из рисунка видно, что  , где
, где  (6)
(6)
Теоретический расход будет меньше, т.к. существуют потери напора, учтём это с помощью поправочного коэффициента, который называется коэффициентом расхода μ.
 , где S1=Sвен (7).
, где S1=Sвен (7).
Подставим в (7) уравнение (5) (с учётом (6)):
 , где
, где 
В итоге имеем:
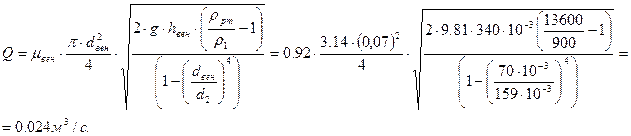
2.4.3.Определим потери напора hА-В.
hА-В=hд+hм (3) , где hд - потери напора по длине трубопровода (м); hм- потери напора от местных сопротивлений.
hм= hкор +hкол+hзад , где hкор- потери напора на коробке всасывающей линии (м);
hкол- потери напора на колене всасывающей линии (м);
hзад- потери напора на задвижке всасывающей линии (м).
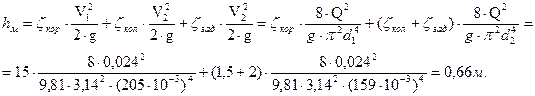
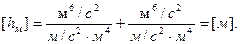
hд=hд1+hд2 , где hд1- потери напора на участке трубопровода l1;
hд2- потери напора на участке трубопровода l2.
 ;
;  ;
; 
где  - коэффициент гидравлического сопротивления для соответствующего участка.
- коэффициент гидравлического сопротивления для соответствующего участка.
Для определения λ1 и λ2 необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Re для этих участков:


где ν- кинематическая вязкость циркуляционной жидкости (м2/с).
Имеем, что Re1>Reкр=2300  на участке трубопровода l1 турбулентный режим течения;
на участке трубопровода l1 турбулентный режим течения;
Re2>Reкр=2300  на участке трубопровода l2 турбулентный режим течения.
на участке трубопровода l2 турбулентный режим течения.
Определим тип трубопровода (шероховатый или гладкий) на участках трубопровода l1 и l2.
Для этого определим значения величин обратной относительной шероховатости для обоих рассматриваемых участков:

Оба участка принадлежат зоне шероховатых труб, т.к. их числа Re принадлежат промежуткам: 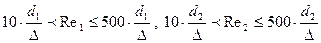
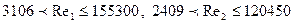 для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:
для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:

Найдём суммарные потери напора для участков l1 и l2:


Подставим полученные нами значения в формулу (3) и получим необходимую величину:
hА-В=hд+hм=0,81+0139,=1,47м.
2.4.4.По формуле (2) определим геометрическую высоту всасывания насоса Н2:


Вариант 26
2.4.1.Запишем уравнение Бернулли для сечения А-А и В-В:

Для определения Н2 необходимо определить потери напора hA-B, расход Q по условию равен 20 л/с.
2.4.2.Определим потери напора hА-В.
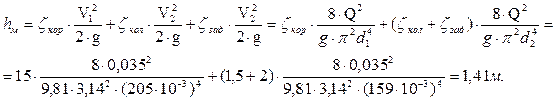
hд=hд1+hд2 , где hд1- потери напора на участке трубопровода l1;
hд2- потери напора на участке трубопровода l2.
 ;
;  ;
; 
где  - коэффициент гидравлического сопротивления для соответствующего участка.
- коэффициент гидравлического сопротивления для соответствующего участка.
Для определения λ1 и λ2 необходимо определить режим течения жидкости на соответствующих участках трубопровода. Для этого определим числа Re для этих участков:


где ν- кинематическая вязкость циркуляционной жидкости (м2/с).
Имеем, что Re1>Reкр=2300  на участке трубопровода l1 турбулентный режим течения;
на участке трубопровода l1 турбулентный режим течения;
Re2>Reкр=2300  на участке трубопровода l2 турбулентный режим течения.
на участке трубопровода l2 турбулентный режим течения.
Определим тип трубопровода (шероховатый или гладкий) на участках трубопровода l1 и l2.
Для этого определим значения величин обратной относительной шероховатости для обоих рассматриваемых участков:

Оба участка принадлежат зоне шероховатых труб, т.к. их числа Re принадлежат промежуткам: 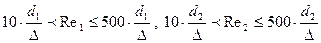
 для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:
для первого и второго промежутков соответственно. Следовательно, для определения λ1 и λ2 воспользуемся формулой Альтшуля:
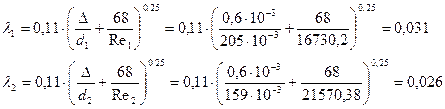
Найдём суммарные потери напора для участков l1 и l2:
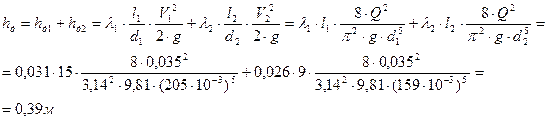

Подставим полученные нами значения в формулу (3) и получим необходимую величину:
hА-В=hд+hм=0,39+1,41=1,8м.
2.4.3.По формуле (2) определим геометрическую высоту всасывания насоса Н2:
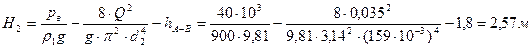

Дата добавления: 2015-04-18; просмотров: 300; Мы поможем в написании вашей работы!; Нарушение авторских прав |