Определение показаний ртутного дифманометра расходомера Вентури.

Вариант 2

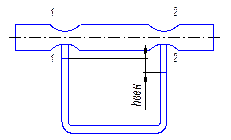Запишем уравнение Бернулли Для двух сечений 1-1 и 2-2:

(1)

где , - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

, - давления в сечениях А-А и В-В соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V₁ ,V₂ - скорость течения жидкости в сеченях А-А и В-В соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

- потери напора на участках между выбранными сечениями.

Выберем ось трубопровода за начало отсчёта, тогда z₁=z₂=0, т.к. трубопровод горизонтален. Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора h_A-B=0.

α₁=α₂=1, (для практических расчётов).

Запишем (1) с учётом всех утверждений:

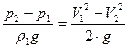(2).

Т.к. расход в сечениях постоянен, то 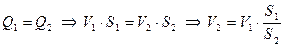(3)

Подставим (3) в (2): (4).

В действительности расход меньше теоретического на безразмерный коэффициент μ=Q/Q_т, тогда V₂ с учётом потерь напора равна:

.

Разность давлений, измеренная дифманометром, определяется из следующего соотношения:

p₂-p₁=(ρ_рт-ρ₁)g∆h , где ρ_рт- плотность ртути (кг/м³).

С другой стороны, разность давлений в сечениях 1-1 и 2-2 расходомера определяется при помощи дифманометра, обычно ртутного, где h=h_рт.

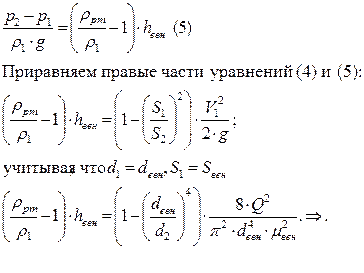
Вариант 14

h_вен известно по условию и равно 340 мм.рт.ст. или 0,340м.

2.8. Определить установившийся уровень жидкости в промежуточной емкости Н₁.

Вариант 2

Н₁ известно по условию и равно 4,2 м.

Вариант 14

Для определения установившегося уровня жидкости в промежуточной ёмкости Н₁ составим уравнение Бернулли для сечений 1-1 и 2-2.

(1)

где , - расстояния от сечений А-А и В-В соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

, - давления в сечениях А-А и В-В соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V₁ ,V₂ - скорость течения жидкости в сеченях А-А и В-В соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях А-А и В-В соответственно;

- потери напора на участках между выбранными сечениями.

Плоскость сравнения совместим с сечением 2-2, тогда z₁=Н₁;z₂=0. Предположим, что по трубопроводу течёт идеальная жидкость, что позволяет не учитывать потери напора h_A-B=0.

α₁₌α₂=1, (для практических расчётов). Т.к. диаметр промежуточной ёмкости во много больше диаметра насадка V₁>>V₂, значит V₁=0, V₂=V_нас.

р₁=р₂=р_атм, т.к. ёмкости открытые.

Запишем (1) с учётом всех утверждений:

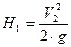(2).

Зная расход можно определить V₂:

(3).

Подставляя (3) в (2):

В действительности при прохождении жидкости в ёмкости через насадок возникают потери напора, учтём их с помощью коэффициента расхода :

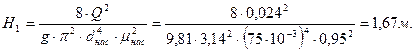
Вариант 26

2.9. Определение разности показаний манометров р_м2 и р_м3.

Вариант 2

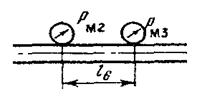Для сечений р_м2 и р_м3 уравнение Бернулли имеет вид:

(1)

где , - расстояния от сечений р_м2 и р_м3 соответственно до некоторой произвольно выбранной горизонтальной плоскости (м);

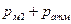( ), ( ) - давления в сечениях р_м2 и р_м3 соответственно (Па);

- плотность циркулирующей жидкости (кг/м³);

g - ускорение свободного падения (м²/с);

V₂ ,V₃ - скорость течения жидкости в сечениях р_м2 и р_м3 соответственно (м/с);

, - коэффициенты Кориолиса, которые учитывают неравномерность распределения скоростей в сечениях р_м2 и р_м3 соответственно;

- потери напора на участках между выбранными сечениями.

Выберем ось трубопровода за начало отсчёта, тогда z₂=z₃=0, т.к. трубопровод горизонтален.

α₁₌α₂=1, (для практических расчётов).

Потери напора между выбранными сечениями определяются только потерями напора по длине трубопровода, т.к. местных сопротивлений на данном участке нет

V₂ =V₃ , т.к. расход и площадь поперечного сечения одинакова для сечений р_м2 и р_м3.

В итоге (1) примет вид:

(2)

Потери напора по длине трубопровода определяются по формуле Дарси-Вейзбаха:

(3).

Подставим (3) в (2):

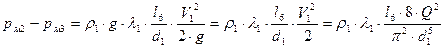(4).

Коэффициент гидравлического сопротивления λ=0,0247 (см. пункт 2.3.3).

Подставим в (4) значения параметров и получим конечный результат:

Вариант 14

Вариант 26