
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение суммарных потери напора в местных сопротивлениях нагнетательной линии и их суммарную эквивалентную длину.
Вариант 2
Потери напора в местных сопротивлениях складываются из потерь на фланце, в угольниках, расходомера Вентури, на задвижке и выходе из трубы. Из справочника найдём значения коэффициенты местных сопротивлений: ζфл=0,1; ζуг=1,32; ζвен=2; ζвых=0,5.
Запишем формулу Вейзбаха для нагнетательной линии:

В нашем случае имеем (с учётом  ):
):
 (1)
(1)
Потери напора в местных сопротивлениях можно выразить через эквивалентную длину, т.е. такую длину трубопровода для которой hд=hм.сопр. и 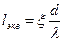 .
.
Суммарная эквивалентная длина определяется по формуле:
 (2)
(2)
Подставим значения параметров в (1) и (2):


Вариант 14


Вариант 26


2.11. Определение необходимого диаметра самотечного трубопровода dc, обеспечивающего установление заданного постоянного уровня в верхнем резервуаре Н3.
Вариант2
Для определения dc будем использовать графоаналитический способ решения с использованием ПК (программа Microsoft Exсel). Задаёмся интервалом dci от 1мм до 20см с шагом 1мм. И для каждого варианта рассчитаем потери напора возникающих при прохождение жидкости по самотёчному трубопроводу.
Потери напора определяются по формуле:  , где
, где 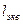 - суммарная эквивалентная длина местных сопротивлений самотёчного трубопровода.
- суммарная эквивалентная длина местных сопротивлений самотёчного трубопровода.
Вычислим поэтапно потери напора для dc от 0 до 200 мм:
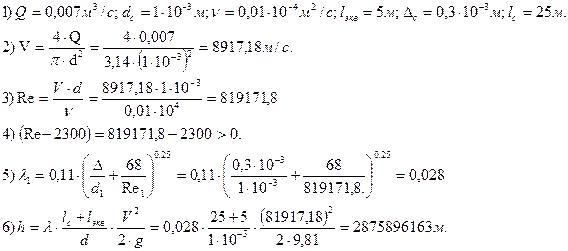
По результатам вычисления ПК  составим таблицу и построим график зависимости h=f(
составим таблицу и построим график зависимости h=f(  ).
).
| d, м | 0,1 | 0,105 | 0,11 |
| h, м | 5,736 | 4,49 | 3,562 |

Для определения необходимого значения диаметра трубопровода по полученному графику определяем  для значения h=H2+H3=cons=3.243+0,8=4,243 м, т.к. уровень установившейся – это и есть потери напора при прохождение жидкости по самотёчному трубопроводу.
для значения h=H2+H3=cons=3.243+0,8=4,243 м, т.к. уровень установившейся – это и есть потери напора при прохождение жидкости по самотёчному трубопроводу.
Имеем, что при h=4,243м значение диаметра примерно равно 
Вариант 14
Вычислим поэтапно потери напора для dc=1мм:
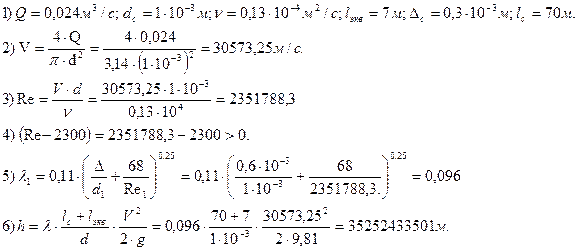
По результатам вычисления ПК  составим таблицу и построим график зависимости h=f(
составим таблицу и построим график зависимости h=f(  ).
).
| d,м | 0,12 | 0,125 | 0,13 | 0,135 | 0,14 |
| h,м | 6,29 | 5,11 | 4,18 | 3,44 | 2,86 |

Для определения необходимого значения диаметра трубопровода по полученному графику определяем  для значения h=H2+H3=cons=2,985+3,5=6,485м, т.к. уровень установившейся – это и есть потери напора при прохождение жидкости по самотёчному трубопроводу.
для значения h=H2+H3=cons=2,985+3,5=6,485м, т.к. уровень установившейся – это и есть потери напора при прохождение жидкости по самотёчному трубопроводу.
Имеем, что при h=6,485м значение диаметра примерно равно 
Вариант 26
Вычислим поэтапно потери напора для dc=1мм:

По результатам вычисления ПК  составим таблицу и построим график зависимости h=f(
составим таблицу и построим график зависимости h=f(  ).
).
| d, м | 0,07 | 0,075 | 0,08 |
| h, м | 3,573 | 2,531 | 1,776 |

Для определения необходимого значения диаметра трубопровода по полученному графику определяем  для значения h=H2+H3=cons=2,57+3,5=3,07м, т.к. уровень установившейся – это и есть потери напора при течение жидкости по самотёчному трубопроводу.
для значения h=H2+H3=cons=2,57+3,5=3,07м, т.к. уровень установившейся – это и есть потери напора при течение жидкости по самотёчному трубопроводу.
Имеем, что при h=3,07м значение диаметра примерно равно 
2.11. Определение минимальной толщины стальных стенок трубы d2, при которой не происходит её разрыва в момент возникновения прямого гидравлического удара.

Вариант2
Опасным сечением для трубы будет ее любое диаметральное сечение.
Силу давления жидкости на цилиндрическую поверхность abс определяют пренебрегая весом жидкости как силу давления жидкости на проекцию цилиндрической поверхности и на диаметральную плоскость ас по формуле:
 , где p – давление. (*)
, где p – давление. (*)
Эта сила давления воспринимается двумя сечениями стенки трубы, поэтому

где σдоп – допустимое напряжение для материала трубы. Из формулы (*) определяем минимальную толщину стенки трубы:
(**) 
где p = pм1+Δр, υ = 4·Q/(π·d2), d = d2, Δр = сυρ – формула Жуковского. Для стальных труб с = 1200 м/с. σдоп для стали 20 равна 0,16·109 Па.
 Таким образом, окончательная формула примет вид:
Таким образом, окончательная формула примет вид:
(***)
 |
Вариант 14
Согласно формуле (***) имеем:

Вариант 26
 Согласно формуле (***) имеем:
Согласно формуле (***) имеем:
Дата добавления: 2015-04-18; просмотров: 536; Мы поможем в написании вашей работы!; Нарушение авторских прав |