Закон Архимеда. Закон Архимеда — это сила с которай жидкасть действует на погруженнае в нее тела равно весу жидкости в обеме погруженого тела.

Закон Архимеда — это сила с которай жидкасть действует на погруженнае в нее тела равно весу жидкости в обеме погруженого тела.

R=-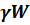

W-обьем тела.

Где -плотность тела

G-ускорение совободного подение.

Вопрос

Основные элементы движения жидкости. Причинами движения жидкости являются действующие на нее силы: объемные или массовые силы (сила тяжести, инерционные силы) и поверхностные силы (давление, трение). В отличие от гидростатики, где основной величиной, характеризующей состояние покоя жидкости, является гидростатическое давление, которое определяется только положением точки в пространстве, т.е. , в гидродинамике основными элементами, характеризующими движение жидкости, будут два: гидродинамическое давление и скорость движения (течения) жидкости.

Гидродинамическое давление р – это внутреннее давление. развивающееся при движении жидкости. Скорость движения жидкости в данной точке и – это скорость перемещения находящейся в данной точке частицы жидкости, определяемая длиной пути l, пройденного этой частицей за единицу времени t.

В общем случае основные элементы движения жидкости р и и для данной точки зависят от ее положения в пространстве (координат точки) и могут изменяться во времени. Аналитически это положение гидродинамики записывает

11. Гидровлические элементы потока. Скорасть и расход жидкости.

Поток- это савакупнасть элементарных струек в платную прилегающие дуг к другу и образующих сплашную массу движущейся жидкости.

Скорасть жидкости у различных точках поперечного сечения потока( местная скорасть) может быть не одинаковы поэтыму для хороктеристики дыижении всего потокавводится в расмотрении среднего по всему сечению скорасть потока.

Vср=

Расход потока жидкости равен средней скорасти умноженай на площадь его поперечного сечения.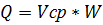

12.Уравнение Бернулли для идеальной и реальной жидкости.Основные уравнение равномерного движения.

Для идеальной жидкости.

Уравнение Бернулли, дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости.

∆Z+∆P/ϫ+∆υ2/2*g=0

z1 и z2 - удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и 2-2;

- удельные энергии давления, характеризующие потенциальную энергию давления в тех же сечениях;скоростная высота или скоростной напор.

- удельные кинетические энергии в тех же сечениях.

H-полный напор.

Для реал.жидкости.

α1 и α2,-называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Основные уравнение равномерного движения.

Вопрос 13. Гидравлические сопротивления и их виды

Различают два вида гидравлических сопротивлений:

-местные

-линейные

Линейные потери происходят при движении жидкости по трубе или каналу. При этом, на каждом участке силы трения совершают работу и теряется напор.

Местные потери характеризуются потерями энергии на относительно компактном участке. Примерами таких участков могут быть вентили, задвижки, клапаны, повороты, внезапные расширения или сужения трубы.

Вопрос 14. Режимы движения жидкостей, число Рейнольдса

Режимы движения жидкости:

Ламинарное (упорядоченное) -при котором отдельные слои жидкости скользят друг относительно друга не смешиваясь между собой.

Турбулентное (неупорядоченное) - частицы жидкости движутся по сложным все время изменяющимся траекториям и в жидкости происходит интенсивное перемешивание.

Число Рейнольдса - безразмерное число от которого зависит режим потока жидкости в трубе.

1.Средняя скорость V

2.Диаметр трубы d

3.Плотность жидкости ρ

4. Абсолютная вязкость μ

15. При определений кофициентов гидравлических трений для групп круглого сечения может пользоватся подстовляя между диномических и гидровлических радиусов. При ламинпрном течений в круглых трубах кафициент гидровлическое трение вычесляют по этой формуле 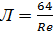.А для труб любой формы сечения Л= . Где А это кофициент чисел значение которого зависит от формы сечения трубы d . Определения потерь напора по длине h= .Местные потери напора обуславливает приодолением местных сопративлений создоваемыми местными потерями и трубопроводных сетей. Местные вызывают изменения велечены или напровления движения жидкости на отдельных участках что связоно с появлениям потери напора. Движения в трубопроводе при наличий местных сопративлений являются не равномерным. Определения местных потерь напора hm= . V-это скорость течения правильно расположена ниже по течению за даными сопративлениями. Определять давления . Потеря напора давления при внезапном расширений. V1 и V2 – скорость сечения до и после расширения.

16. При турбулентном режиме движении потери напора по длине зависят от состояния стенок, ограничивающих поток. Потери напора на трение по длине потока, возникающие при равномерном напорном движении жидкости в трубах, определяют по уравнению где l – длина участка трубы, м; d – внутренний диаметр трубопровода, м; v – средняя скорость потока, м/сек; g – ускорение свободного падения, м/сек2; – безразмерный коэффициент гидравлического трения. В уравнении остается не выясненным смысл безразмерного коэффициента . Для выяснения физического смысла коэффициента при равномерном напорном движении жидкости в трубах, и при турбулентном режимах движения используем уравнение Д. Бернулли. Распределение скоростей в сечениях одинаково, частицы жидкости двигаются без ускорений. Потери напора при турбулентном движении. В инженерной практике чаще встречается турбулентный режим движения жидкости в трубах, которые труднее исследовать теоретически. При турбулентном режиме наблюдается интенсивное вихреобразование, частицы жидкости описывают сложные траектории, местные скорости меняются во времени даже при постоянном расходе. Это явление называется пульсацией скорости. Часть кинетической энергии жидкости переходит в тепловую. Мгновенные скорости пульсируют около своего осредненного значения, которое за достаточно длительный промежуток времени остается постоянным; это значение и называется осредненной скоростью. Очевидно, что чем меньше диаметр, тем быстрее частицы жидкости совершат пробег от центра трубопровода к стенкам и встретятся с бугорками шероховатости, и, отражаясь от них, вызовут возмущения в потоке жидкости. Следовательно, частота вихреобразования при малых диаметрах труб больше, и шероховатость той же высоты проявляется сильнее. Это вытекает и из теоретических исследований. Трубы же, в которых коэффициент зависит только от числа Рейнольдса и не зависит от относительной шероховатости, что бывает при сравнительно малых Re и k/d, называют гидравлически гладкими. При этом один и тот же трубопровод в одних условиях может быть гидравлически гладким, а в других – вполне шероховатым. Условия, в которых зависит и от относительной шероховатости, называются переходной областью. Свойства поверхности стенок трубопровода в этом случае не влияют на сопротивление, и зависимость выражается в координатах прямой.

17.Трубопрово́д — инженерное сооружение, предназначенное для транспортировки газообразных и жидких веществ, пылевидных и разжиженных масс^[1], а также твёрдого топлива и иных твёрдых веществ в виде раствора под воздействием разницы давлений в поперечных сечениях трубы

Виды трубопровода :

Водопровод — предназначен для обеспечения водой населения, промышленных предприятий, транспорта^[9].

Воздухопровод — часто создается в рамках промышленного предприятия для обеспечения производства сжатым воздухом

Газопровод — предназначен для транспортировки попутного нефтяного, природного и искусственного газа

Нефтепровод — предназначен для транспортировки сырой нефти. Нефть при этом подвергается подогреву, препятствующему затвердеванию входящих в её состав парафинов

Паропровод — технологический трубопровод, предназначенный для передачи пара под давлением, используемого для отопления или работы сторонних механизмов

Теплопровод (см. тепловая сеть) — предназначен для передачи теплоносителя (вода, водяной пар) от источника тепловой энергии в жилые дома, общественные здания и промышленные предприятия^[

18. Трубопроводы служат для транспортирования различных жидкостей на различные расстояния. Гидравлический расчет трубопроводов базируется на основных уравнениях гидравлики. При расчете длинных трубопроводов пренебрегают потерями напора на местных сопротивлениях, которые малы и обычно не превышают 5 % от общих потерь.Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях одинакова и α₁ = α₂, то скоростной напор можно не учитывать. При этом получим или Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором Н_потр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором Н_расп. Такой напор складывается из геометрической высоты H_потр, на которую поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую эквивалентную геометрическую высоту

а последнее слагаемое Σh - как степенную функцию расходаΣ^{h = KQm}тогдаH_потр = H_ст + KQ^m где K - величина, называемая сопротивлением трубопровода;
Q –расход жидкости;
m - показатель степени, который имеет разные значения в зависимости от режима течения.Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно где l_расч = l + l_экв.Численные значения эквивалентных длин l_экв для различных местных сопротивлений обычно находят опытнымпутем.Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем

По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор Н_потр. При ламинарном течении эта кривая изображается прямой линией при турбулентном - параболой с показателем степени равном двум

19. Методика расчёта «коротких» трубопроводов

короткие трубопроводы расчитывают непосредствено по уровнению Бернули представленому в виде

+ƩБζ

Здесь Б= - величина зависящая от расчетного диаметра трубу

ζ- коофициент местных сопротивлений

- удельное сопротивление трубы

l- длинны участков трубопровода

- пиезометрические напоры в начале и в конце трубопровода, определяемые по формуле

H= ,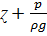

где ɀ- геодезическая отметка какой либо точки трубопровода

p- избыточное давление в этой точке

-пиезометрическпя высота

При скоростях движения воды в трубе v<1.2м/с удельное сопротивления

где 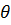- поправочный коофициент, определяемый в зависимости от скорости

20. Расчёт простого и сложного трубопроводов

В гидравлике различают простые и сложные трубопроводы. Простым называется такой трубопровод, который служит для подачи жидкости из одного резервуара в другой без ответвлений. Простой трубопровод может иметь по всей длине одинаковое сечение, а может состоять из ряда последовательно соединенных труб различного сечения.

Сложными называются трубопроводы, имеющие ответвления или состоящие из нескольких линий. Их расчет значительно сложнее, чем простых. Однако, некоторые задачи, относящиеся к сложным трубопроводам, можно решать, рассматривая отдельные их элементы, как простые.

Сложный трубопровод Расчитывают по формуле:

+ * + )

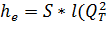Расход жидкости может производиться в какой-либо определенной точке трубопровода, например, на его конце. Такой расход называется транзитным. В некоторых трубопроводах, например, в водопроводах, расход жидкости производится во многих точках по длине. В этих случаях расход называется путевым.

В зависимости от характера сопротивлений трубопроводы подразделяют на длинные и короткие. В длинных трубопроводах потери напора по длине во много раз больше потерь от местных сопротивлений, которые составляют 2—5% от общих потерь энергии в трубопроводе.

В так называемых коротких трубопроводах потери напора от местных сопротивлений велики по сравнению с потерями по длине трубопровода. Принятая классификация позволяет в значительной степени упростить гидравлический расчет трубопроводов.

С учетом указанных условий приведены методики расчета напорных, т. е. заполненных по всему сечению трубопроводов, при установившемся равномерном движении жидкости.