Уравнение Бернулли для струйки идеальной жидкости. Геометрический и физический смысл уравнения Бернулли.

Рассмотрим элементарную струйку реальной жидкости также при установившемся движении.

При движении элементарной струйки реальной жидкости общий запас удельной механической энергии не может оставаться постоян­ным, как это рассматривалось при движении идеальной жидкости. Дело в том, что при движении реальной жидкости вследствие ее вязкос­ти возникают сопротивления движению, на преодоление которых зат­рачивается часть механической энергии.

При продвижении от одного сечения к другому удельная энергия в струйке (а значит, и напор) будет уменьшаться. Энергия в первом (вы­шерасположенном по течению) сечении при движении вязкой жидкос­ти всегда больше, чем во втором (нижерасположенном) сечении, на значение потерь удельной энергии между этими сечениями. Поте­ри удельной энергии можно выразить через потери напора h_тр. Как и все остальные члены уравнения (1.55), h_тр имеет линейную размер­ность. Окончательно уравнение Бернулли для струйки реальной жид­кости имеет вид:

(1.56)

т.е. отличается от (1.54) наличием потерь напора. В этом случае напорная линия (линия удельной энергии) будет снижаться по направлению движения.

Геометрическая интерпретация уравнения БернуллиПоложение любой частицы жидкости относительно некоторой произвольной линии нулевого уровня 0-0 определяется вертикальной координатой Z. Для реальных гидравлических систем это может быть уровень, ниже которого жидкость из данной гидросистемы вытечь не может. Например, уровень пола цеха для станка или уровень подвала дома для домашнего водопровода.

• Как и в гидростатике, величину Z называют нивелирной высотой.
• Второе слагаемое - носит название пьезометрическая высота. Эта величина соответствует высоте, на которую поднимется жидкость в пьезометре, если его установить в рассматриваемом сечении, под действием давления P.
• Сумма первых двух членов уравнения 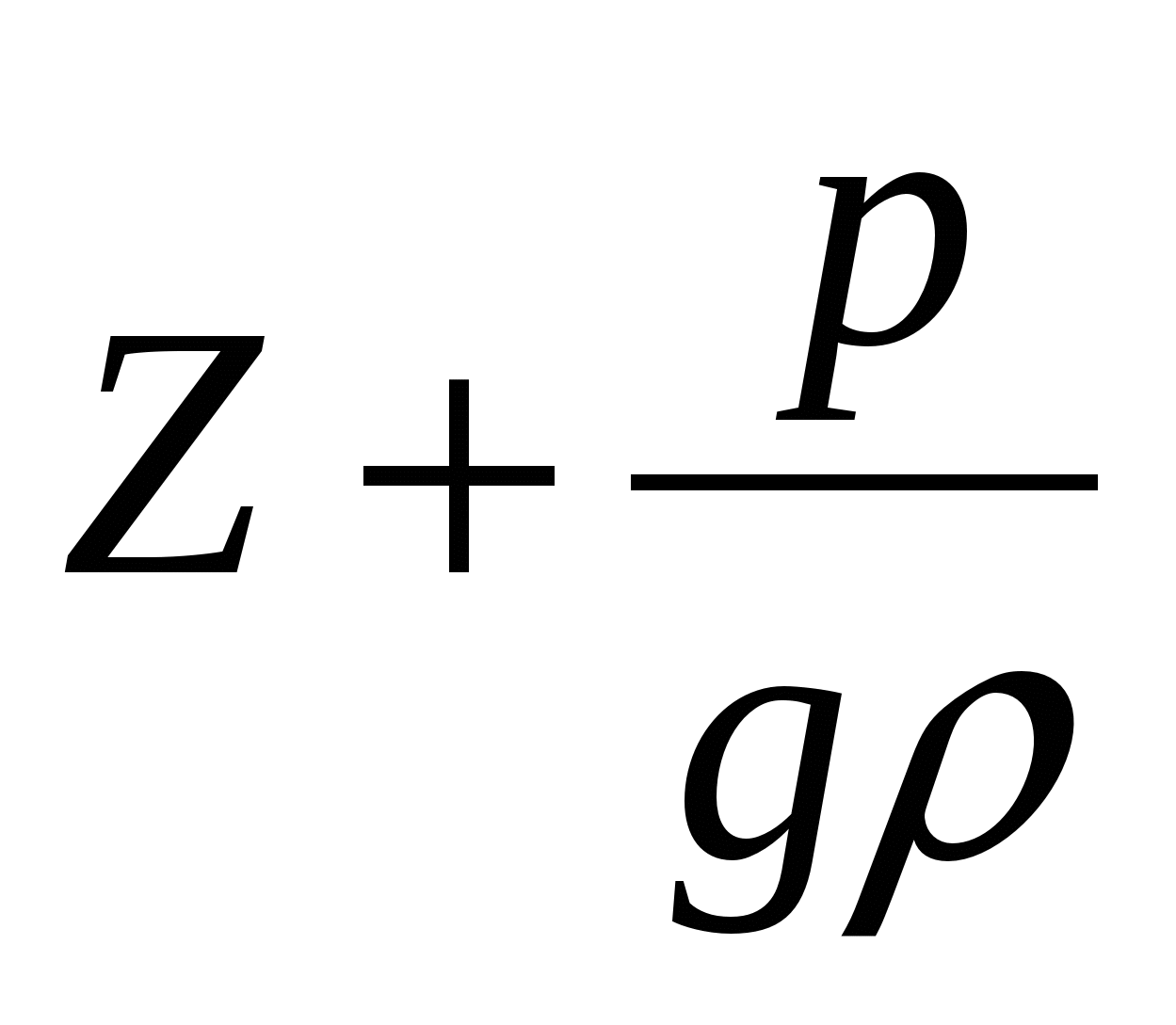¾ гидростатический напор.
• Третье слагаемое в уравнения Бернулли называется скоростной высотой или скоростным напором. Данную величину можно представить как высоту, на которую поднимется жидкость, начавшая двигаться вертикально со скорость u при отсутствии сопротивления движению.
• Сумму всех трёх членов (высот) называют гидродинамическим или полным напором и, как уже было сказано, обозначают буквой Н.

Физический смысл уравнения Бернулли

· Согласно уравнению Бернулли сумма трех указанных величин является постоянной, что приводит к равенству: de1= de2.

· Итак, сумма трех членов уравнения Бернулли есть сумма трех удельных энергий: удельной кинетической энергии, удельной потенциальной энергии давления и удельной потенциальной энергии положения. Для идеальной жидкости сумма трех удельных энергий по длине элементарной струйки – постоянна.

· В общем, уравнение Бернулли является специальным выражением основного физического закона сохранения энергии