Графическое представление уравнения Бернулли для струйки идеальной и реальной жидкости.

Предварительно рассмотрим измерительный прибор - трубку Пито. Этот прибор представляет собой открытую с 2-х сторон стеклянную трубку, изогнутую под прямым углом. В нижней части трубка несколько сужена для ослабления удара при входе в нее жидкости. Трубка Пито служит для измерения скорости течения за счет дополнительного давления (по сравнению с давлением в пьезометрической трубке), возникающего вследствие скоростного напора. Если в каком-либо сечении потока жидкости установить две трубки - пьезометрическую и трубку Пито (см. рис. 2.20), то высота подъема жидкости в трубке Пито будет больше высоты подъема жидкости в пьезометрической трубке на величину скоростного напора V¹ 12%.

Графически уравнение Бернулли можно представить следующим образом. Рассмотрим поток жидкости, выберем плоскость сравнения, сечения потока (см. рис. 2.21). В выбранных сечениях установим пьезометрические трубки и трубки Пито. Все члены уравнения Бернулли будут представлены графически.

Пьезометрический уклон Iр на участке между сечениями 1 и 2 определяется по формуле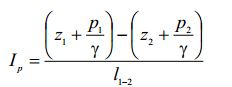

Величина пьезометрического уклона может быть как положительной, так и отрицательной. Отрицательной будет в том случае, когда поток расширяется. Соединив уровни жидкости в трубках Пито, получим линию давления, или напорную линию (гидродинамическую линию, линию полных удельных энергий).Изменение полной удельной энергии потока, приходящееся на единицу длины, называется гидравлическим уклоном. Он характеризует величину потерь давления, приходящихся на единицу длины.

Гидравлический уклон является всегда величиной положительной.

29. Уравнение Бернулли для потока реальной жидкости. При переходе от уравнения Бернулли для элементарной струйки идеальной жидкости к уравнению потока реальной жидкости необходимо учитывать неравномерность распределения скоростей по сечению потока и потери энергии жидкости на внутреннее трение, что обусловлено вязкостью жидкости. В реальной жидкости вязкость создает сопротивление движению жидкости. Это вызывает появление дополнительных потерь напора (энергии потока), которые будем обозначать h пот. Распределение скоростей элементарных струек в потоке обычно неизвестно, поэтому в уравнение Бернулли вводят поправочный коэффициент α, учитывающий изменение кинетической энергии вследствие неравномерности распределения скоростей в живом сечении потока. Коэффициент α называется коэффициентом кинетической энергии или коэффициентом Кориолиса и определяется обычно опытным путем. Для установившегося движения жидкости среднее значение коэффициента α принимается равным 1,05–1,11 при турбулентном режиме, при ламинарном режиме α=2. Уравнение Бернулли для двух сечений потока реальной жидкости имеет вид

В уравнении Бернулли для элементарной струйки реальной жидкости значение коэффициента α = 1.

Уравнение Бернулли для потока реальной жидкости с физической точки зрения представляет уравнение энергетического баланса. Теряемая энергия превращается в тепловую.