Энтропия

Основные подходы к измерению количества информации.

Энтропия как мера степени неопределенности.

Энтропия - это мера степени неопределенности состоянии системы X (случайной величины) с конечным или счетным числом исходов.

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

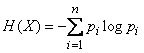. (18.2.2)

Энтропия , как мы увидим в дальнейшем, обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие - невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний - увеличивается. Наконец, и это самое главное, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.

Логарифм в формуле (18.2.2) может быть взят при любом основании . Перемена основания равносильна простому умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 - о «двоичных единицах». На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах; это хорошо согласуется с применяемой в электронных цифровых вычислительных машинах двоичной системой счисления.

В дальнейшем мы будем везде, если не оговорено противное, под символом понимать двоичный логарифм.

В приложении (табл. 6) даны двоичные логарифмы целых чисел от 1 до 100.

Легко убедиться, что при выборе 2 в качестве основания логарифмов за единицу измерения энтропии принимается энтропия простейшей системы , которая имеет два равновозможных состояния:

Таблица 2

Действительно, по формуле (18.2.2) имеем:

.

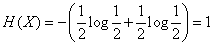Определенная таким образом единица энтропии называется «двоичной единицей» и иногда обозначается bit (от английского «binary digit» - двоичный знак). Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.

Измерим в двоичных единицах энтропию системы , которая имеет равновероятных состояний:

Таблица 3

Имеем:

или

, (18.2.3)

т. е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.

Например, для системы с восемью состояниями .

Докажем, что в случае, когда состояние системы в точности известно заранее, ее энтропия равна нулю. Действительно, в этом случае все вероятности 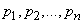в формуле (18.2.2) обращаются в нуль, кроме одной - например , которая равна единице. Член обращается в нуль, так как . Остальные члены тоже обращаются в нуль, так как

.

а максимальная энтропия системы равна:

, (18.2.8)

т. е. максимальное значение энтропии системы с конечным числом состояний равно логарифму числа состояний и достигается, когда все состояния равновероятны.

Вычисление энтропии по формуле (18.2.2) можно несколько упростить, если ввести в рассмотрение специальную функцию:

, (18.2.9)

где логарифм берется по основанию 2.

Формула (18.2.2) принимает вид:

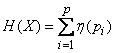. (18.2.10)

Функция затабулирована; в приложении (табл. 7) приведены ее значения для от 0 до 1 через 0,01.

Среднее значение (математическое ожидание) случайной величины - и есть, как нетрудно убедиться, энтропия системы . Для ее получения значения (18.2.12) осредняются с «весами», равными соответствующим вероятностям .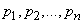

Формулы, подобные (18.2.11), где энтропия представляется в виде математического ожидания, позволяют упрощать преобразования, связанные с энтропией, сводя их к применению известных теорем о математических ожиданиях.

Энтропия сложных событий.

Если требуется оценить меру неопределенности сложных опытов, состоящих из целой совокупности следующих друг за другом испытаний, то необходимо иметь правило сложения энтропии. Допустим мы осуществляем два независимых опыта α.и β

Н(αβ) = Н(α.) + Н(β).

Это равенство называется правилом сложения энтропии независимых опытов.

Если отказаться от условий независимости опытов α и β, то мы придем к понятно условной энтропии.

При этих условиях энтропия сложного опыта αβ не будет равна сумме энтропии α и β. Например, в случае если опыт αβ состоит в последовательном извлечении шаров из урны, содержащей всего два разноцветных шара. В этом случае после выполнения опыта α опыт β уже не будет содержать никакой информации и энтропия сложного опыта αβ будет равна энтропии одного опыта α, а не сумме энтропии опыта α. и β.

Условной энтропией опыта β при условии выполнения опыта α или условной энтропии опыта α при условии выполнения опыта β считается соответственно Н_α(β) и Н_β(α):

Н_α(β) = р(А₁)Н_А1(β)+р(А₂) Н_А2(β)+ ….+ р(АK)Н_Аk(β),

где Н_Аk(β) – условная энтропия опыта β при условии А_k.

Таким образом, формула для подсчета энтропии Н(αβ) сложного опыта α β, в случае зависимости опытов α и β, имеет вид

Н(αβ)=Н(α)+Н_α(β).

Данное выражение называется правилом сложения энтропии для зависимых опытов.