Модель системы безопасности HRU. Основные положения модели. Теорема об алгоритмической неразрешимости проблемы безопасности в произвольной системе.

Модель HRU используется для анализа системы защиты, реализую­щей дискреционную политику безопасности, и ее основного элемента - матрицы доступов. При этом система защиты представляется конечным ав­томатом, функционирующим согласно определенным правилам перехода.

Модель HRU была впервые предложена в 1971 г. В 1976 г. появилось формальное описание модели.

Обозначим: О-множество объектов системы; S-множество субъек­тов системы (SÍO); R- множество прав доступа субъектов к объектам, например права на чтение (read), на запись (write), владения (own); M-матрица доступа, строки которой соответствуют субъектам, а столбцы -объектам; 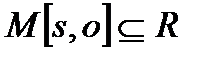- права доступа субъекта s к объекту о.

Отдельный автомат, построенный согласно положениям модели HRU, будем называть системой. Функционирование системы рассматри­вается только с точки зрения изменений в матрице доступа. Возможные изменения определяются шестью примитивными операторами: внести право, удалить право, создать субъекта, создать объект, уничтожить субъект, уничтожить объект.

В результате выполнения примитивного оператора α осуществляется переход системы из состояния Q = (S,O,M) в новое состояние 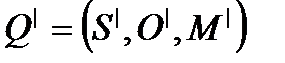. Данный переход обозначим через Q├_aQ'. Из примитивных операторов могут составляться команды, каждая из которых состоит из двух частей: условия, при котором выполняется команда, последовательности примитивных операторов.

Однако, как показывают результаты анализа модели HRU, задача построения алгоритма проверки безопасности сис­тем, реализующих дискреционную политику разграничения прав доступа, не может быть решена в общем случае.

Обозначим состояние безопасности системы:

Определение 1. Будем считать, что возможна утечка права rÎR? в ре­зультате выполнения команды с, если при переходе системы в состояние Q' выполняется примитивный оператор, вносящий r в элемент матрицы доступов М, до этого r не содержавший.

Определение 2. Начальное состояние Q₀ называется безопасным по отношению к некоторому праву r, если невозможен переход системы в такое состояние О, в котором может возникнуть утечка права r.

Теорема.Задача проверки безопасности произвольных систем ал­горитмически неразрешима.

Доказательство. Для доказательства теоремы воспользуемся фак­том, доказанным в теории машин Тьюринга: не существует алгоритма проверки для произвольной машины Тьюринга и произвольного начально­го слова остановится ли машина Тьюринга в конечном состоянии или нет.

Под машиной Тьюринга понимается способ переработки слов в ко­нечных алфавитах. Слова записываются на бесконечную в обе стороны ленту, разбитую на ячейки. Суть: При сопоставлении машины Тьюринга и модели HRU, элементы и команды машины Тьюринга представляются в виде элементов и команд модели HRU. Зададим матрицу дос­тупов М в текущем состоянии. Для каждой команды машины Тьюринга задается соответствующая ей команда модели HRU. Если машина Тьюринга останавливается в своем конечном состоя­нии, то в соответствующей системе, построенной на основе модели HRU, происходит утечка права доступа. Из алгоритмической неразре­шимости задачи проверки - остановится ли машина Тьюринга в конечном состоянии, следует аналогичный вывод для задачи проверки безопасно­сти соответствующей ей системы HRU. Таким образом, в общем случае для систем дискреционного разграничения доступа, построенных на осно­ве модели HRU, задача проверки безопасности алгоритмически неразре­шима.

Дальнейшие исследования модели HRU велись в основном в на­правлении определения условий, которым должна удовлетворять систе­ма, чтобы для нее задача проверки безопасности была алгоритмически разрешима. Так, в 1976 г. было доказано, что эта задача разрешима для систем, в которых нет операции "создать". В 1978 г. показано, что таковыми могут быть системы монотонные и моноусловные, т.е. не со­держащие операторов "уничтожить" или "удалить" и имеющие только ко­манды, части условия которых имеют не более одного предложения. В том же году показано, что задача безопасности для систем с конеч­ным множеством субъектов разрешима, но вычислительно сложна.

Модель распространения прав доступа Take-Grant. Теоремы о передаче прав в графе доступов, состоящем из субъектов, и произвольном графе доступов. Расширенная модель Take-Grant и ее применение для анализа информационных потоков в АС.