
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоремы о передаче прав в графе доступов, состоящем из субъектов, и произвольном графе доступов.
В модели Take-Grant основное внимание уделяется определению условий, при которых в системе возможно распространение прав доступа определенным способом.
• способа санкционированного получения прав доступа;
• способа похищения прав доступа.
----Санкционированное получение прав доступа.
Данный способ характеризуется тем, что при передаче прав доступа не накладываются ограничения на кооперацию субъектов системы, участвующих в этом процессе.
Пусть х, уÎО - различные объекты графа доступа G0=(S0,O0,E0), aÍR. Определим предикат "возможен доступ" (a,х,у, G0), который будет истинным тогда и только тогда, когда существуют графы G1=(S1,O1,E1),.... Gn=(Sn,On,En), такие, что:
G0├op1 G1├op2…├opN Gn и (x,y,a)ÎEn.
Определение 1. Говорят, что вершины графа доступов являются tg-связными или что они соединены tg-путем, если (без учета направления дуг) в графе между ними существует такой путь, что каждая дуга этого пути помечена t или g. Будем говорить, что вершины непосредственно tg-связны, если tg-путъ между ними состоит из единственной дуги.
Теорема 1. Пусть G0=(S0,O0,E0) - граф доступов, содержащий только вершины-субъекты. Тогда предикат "возможен доступ" (a,х,у,G0) истинен тогда и только тогда, когда выполняются следующие условия 1 и 2.
Условие 1. Существуют субъекты sl .... sm, такие, что (si,y,gi,)ÎE0 для i=1,...,m и a = g1È…Ègm.
Условие 2. Субъект х соединен в графе G0 tg-путем с каждым субъектом si, для i=1,...,m.
Для определения истинности предиката "возможен доступ" в произвольном графе необходимо ввести ряд дополнительных понятий.
Определение 2. Островом в произвольном графе доступов G0 называется его максимальный tg-связный подграф, состоящий только из вершин субъектов.
Определение 3. Мостом в графе доступов G0 называется tg-путь, концами которого являются вершины-субъекты; при этом словарная запись tg-пути должна иметь вид →t*. ←t*, →t*→g←t*, →t*←g←t*, где символ * означает многократное (в том числе нулевое) повторение.
Определение 4. Начальным пролетом моста в графе доступов G0 называется tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид →t*→g.
Определение 5. Конечным пролетом моста в графе доступов G0 называется tg-путь, началом которого является вершина-субъект; при этом словарная запись tg-пути должна иметь вид →t*.
Теорема 2. Пусть G0=(S0,O0,E0) - произвольный граф доступов. Предикат "возможен доступ"(a,х,у, G0) истинен тогда и только тогда, когда выполняются условия 3, 4 и 5.
Условие 3. Существуют объекты s1,...,sm, такие, что (si,y,gi)ÎE0, i=1,...,m, и a = g1È…Ègm.
Условие 4. Существуют вершины-субъекты x1,...,xm и s1,...,sm, такие, что:
· х=хi или хi, соединен с х начальным пролетом моста для i=1,...,m;
· si=si или si соединен с а конечным пролетом моста для i=1,.... m.
Условие 5. Для каждой пары (хi, si), i=1, ...,m, существуют острова li,1… li,ui, ui³1, такие, что хiÎli,1, siÎli,uiи мосты между островами li,jи li,j+1,ui>j³1.
----Похищениеправ доступа
Способ передачи прав доступа предполагает идеальное сотрудничество субъектов В случае похищения прав доступа предполагается, что передача прав доступа объекту осуществляется без содействия субъекта, изначально обладавшего передаваемыми правами Пусть х,у  О-различные объекты графа доступа Go = (So,O0,Eo), a
О-различные объекты графа доступа Go = (So,O0,Eo), a  RОпределим предикат "возможно похищение" (a,x,y,Go), который будет истинным тогда и только тогда, когда (x,y,a)
RОпределим предикат "возможно похищение" (a,x,y,Go), который будет истинным тогда и только тогда, когда (x,y,a)  Eo и существуют графы
Eo и существуют графы  = (
= (  ),
),  , такие, что
, такие, что
 и (x,y,a)
и (x,y,a) 
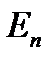 , при этом, если
, при этом, если  (s,y,a)
(s,y,a)  Eo, то
Eo, то  =0,1, , Nвыполняется opK
=0,1, , Nвыполняется opK  granf(a,s,z,y), К=1, N.
granf(a,s,z,y), К=1, N.
Теорема 2.Пусть Go = (So, Oo, Eo)- произвольный граф доступов Предикат "возможно похищение" (a,x,y,Go) истинен тогда и только тогда, когда выполняются условия 3, 4, 5
Условие 3(х,у,а)  Ео
Ео
Условие 4Существуют объекты  , ,sm, такие, что (s,,y,
, ,sm, такие, что (s,,y, 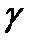 ,)
,)  Eo для i=1, ,т и a =
Eo для i=1, ,т и a = 
Условие 5Являются истинными предикаты "возможен доступ" (t,x, s,Go) для i =1, ,m
Дата добавления: 2015-04-18; просмотров: 329; Мы поможем в написании вашей работы!; Нарушение авторских прав |