Классы вычетов по модулю т

Из свойств 1) — 3) сравнений видно, что отношение сравнимо­сти целых чисел по модулю т является отношением эквивалент­ности, и, следовательно, множество целых чисел разбивается на непересекающиеся классы сравнимых по модулю m чисел. Так как различные остатки при делении на т исчерпываются числами 0,1,2,...,m-1, то получим т классов: 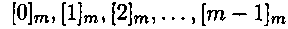(2)где через 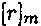обозначен класс всех чисел, которые при делении на т дают в остатке r. Очевидно, что класс 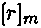однозначно определяется любым одним своим представителем, и потому в даль­нейшем класс 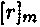будет обозначаться также в виде 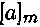, где а — любой представитель этого класса.

Классы (2) называются классами вычетов, а их элементы — вычетами по модулю т. Из определения сравнений следует, что числа из одного класса сравнимы по модулю т, а числа из разных классов не сравнимы по модулю т, т. е.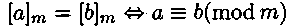

Определение 1. Совокупность чисел, взятых по одному из каждого класса вычетов по модулю т, называется полной систе­мой вычетов по модулю т.

Примером полной системы вычетов по модулю т является множество чисел 0,1,... , m — 1. Это так называемая полная система наименъшцх неотрица­тельных вычетов.

Cледующее свойство полных систем вычетов.

Теорема 1.Если 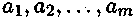есть полная система вычетов по модулю т, число а взаимно простое с т и b— любое целое число, то 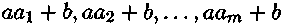(3) есть также полная система вычетов по модулю т.

Доказательство (можно не писать – М.С.). Все числа ряда (3) принадлежат разным классам вычетов по модулю т, поскольку в силу свойств сравнений 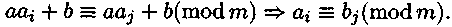А так как в (3) содержится т чисел, т. е. столько же чисел, сколь­ко и классов, то в (3) имеется ровно по одному представителю из каждого класса. Следовательно, (3) есть полная система вычетов по модулю т