Многочлены. Кольцо многочленов над кольцом с единицей. Делимость многочленов, теорема о делении с остатком. Значение и корень многочлена. Теорема Безу.

Пусть - непустое множество, на котором заданы две бинарные операции: сложение и умножение, удовлетворяющие следующим условиям:

1) Структура есть абелева группа, то есть сложение коммутативно и ассоциативно, существует нейтральный элемент (ноль) по сложению и для любого существует единственный противоположный к нему элемент.

2) Структура есть полугруппа, то есть умножение ассоциативно;

3) Операции сложения и умножения связаны законом дистрибутивности: Структура 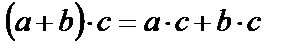и для любых .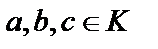

Тогда алгебраическая структура называется кольцом.

Пусть - произвольное кольцо с единицей . Многочленомнад назовем любую бесконечную последовательность элементов 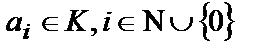, в которой все , за исключением конечного их числа, равны нулю. Элементы назовем коэффициентами многочлена. Многочлен назовем нулевым. Обозначим через 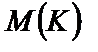множество всех таких последовательностей. Номер последнего ненулевого члена последовательности назовем степенью многочлена и обозначим .

Суммой многочленов называют последовательность , в которой для всех .

Произведением многочленов называют последовательность , в которой для всех .

Произведением многочлена 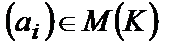на элемент слева или справа называют, соответственно, последовательность или .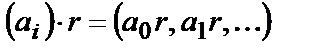

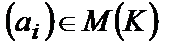Суммой элемента и многочлена называют последовательность .

Во всех последовательностях в вышеприведенных определениях, так же как и в исходных последовательностях, все коэффициенты, за исключением конечного их числа, равны нулю, и потому эти последовательности принадлежат .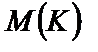

Используя заданные на 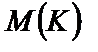операции, можно перейти к традиционной форме записи многочленов. Введем обозначения: , для .

Заметим, что ввиду определения произведения многочленов для любых выполняются равенства:

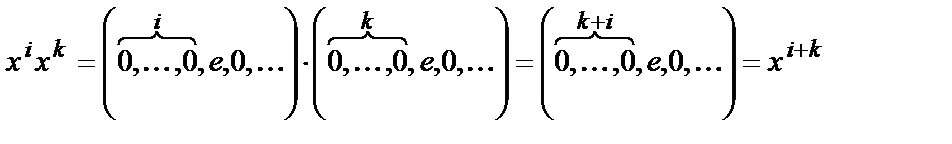
Поэтому для любых верны равенства и для символ обозначает ни что иное, как 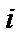-ю степень элемента : .

Пользуясь определением произведения многочлена на элемент множества , получаем, что для любых 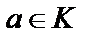и верны равенства 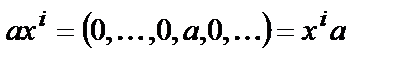, и поэтому любой многочлен может быть записан в виде суммы: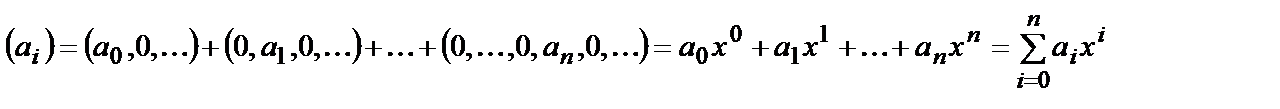

Последнюю запись многочлена 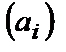можно еще упростить, записав его в общепринятом виде: .

При введенных обозначениях многочлен 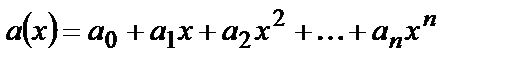называют многочленом от над кольцом ,а элементы называют его коэффициентами. Говорят, что - коэффициент многочлена при , а -его свободный член.Множество 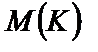называют множеством многочленов от одного переменного над кольцом и обозначают: .

Алгебра многочленов над кольцом с единицей есть кольцо с единицей. Кольцо коммутативно тогда и только тогда, когда кольцо коммутативно, и содержит делители нуля тогда и только тогда, когда содержит делители нуля.

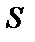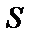Говорят, что элемент кольца делится на элемент слева (справа), если в разрешимо уравнение .

Однако если - кольцо многочленов над кольцом с единицей, то в 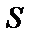можно ввести понятие делимости с остатком и предложить алгоритм, который позволяет проверить, делится один многочлен на другой или нет.

Говорят, что в кольце многочлен делится на многочлен справа с остатком, если существуют многочлены со свойствами , . //(deg–обозначение степени многочлена)

При этом многочлены и называют, соответственно, неполным правым частным и правым остаткомот деления на . Аналогично определяется понятие делимости на слева с остатком.

Если старший коэффициент многочлена обратим в кольце , то любой многочлен можно разделить справа (слева) с остатком на . При этом правые (левые) неполное частное и остаток определяются однозначно.

Если - поле и , то любоймногочлен можно разделить с остатком на и притом единственным способом.

Значением многочлена из в точке называют элемент кольца . Говорят, что - корень многочлена , если .

Данное определение позволяет поставить в соответствие каждому многочлену функцию , определяемую условием .

Очевидно, что значение суммы двух многочленов в любой точке равно сумме их значений. Для произведения многочленов аналогичное утверждение верно не всегда.

Если , 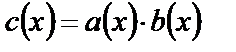и элемент перестановочен со всеми коэффициентами правого множителя , то . При сформулированном условии верны равенства .

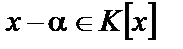Теорема Безу.Остаток от деления справа многочлена на двучлен равен . В частности, элемент

кольца является корнем многочлена тогда и только тогда, когда делится справа на .

Доказательство. //(хз надо или нет) можно разделить справа с остатком на : 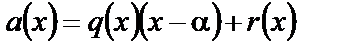, 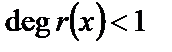. Тогда , где , и 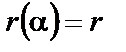. Так как для многочлена 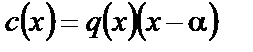верно равенство , то . В частности, равенство эквивалентно равенству 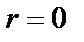, а последнее эквивалентно тому, что делит справа .

Кольца матриц. Матрицы над кольцом и операции над ними. Кольцо квадратных матриц. Определители квадратных матриц над коммутативным кольцом с единицей. Критерий обратимости матрицы над коммутативным кольцом с единицей.