
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Степенные ряды. Первая теорема Абеля. Параметры и радиус сходимости. Равномерная сходимость степенного ряда. Непрерывность суммы. Почленная дифференцируемость. Ряд Тейлора.
Степенные ряды.
Введём понятие степенного ряда
Степенным рядом называется функциональный ряд с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + …
члены которого есть произведения постоянных с0, с1, с2, …, сn, … на степенные функции с целыми показателями степеней от разности (z - z0).
Степенной ряд с центром в точке 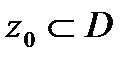 :
:  , где D –область.
, где D –область.
 - ряд с центром в точке z0 = 0 (1)
- ряд с центром в точке z0 = 0 (1)
Введём понятие функционального ряда
Пусть существует последовательность функций f0(x), f1(x), …, fn(x), … . Функциональным рядом будем называть выражение вида f0(x) + f1(x) + … + fn(x) + … .
Теорема Абеля.
1)Пусть степенной ряд (1) сходится в точке  .Тогда он сходится абсолютно в любой точке z, для которой |
.Тогда он сходится абсолютно в любой точке z, для которой |  |<|
|<|  |,и равномерно и абсолютно в любом круге радиуса R:
|,и равномерно и абсолютно в любом круге радиуса R: 
2)Если степенной ряд (1) расходится в точке  , тогда он расходится и во всех точках z таких, что |z|>|
, тогда он расходится и во всех точках z таких, что |z|>|  |.
|.
Доказательство:
Необходимый признак сходимости ряда (Не является достаточным):  при
при 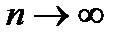
По условию, ряд  сходится, следовательно,
сходится, следовательно, 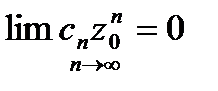 . Любая последовательность, имеющая предел, ограничена, значит, существует такое число M:
. Любая последовательность, имеющая предел, ограничена, значит, существует такое число M:  для всех n=0, 1,… (2)
для всех n=0, 1,… (2)
Ряд (1) запишем в виде 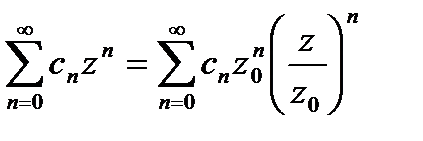
Учитывая неравенства (2) найдем 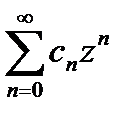 , т.к.
, т.к.  .
.
Здесь  , поэтому последний ряд сходится, а это означает, что сходится ряд
, поэтому последний ряд сходится, а это означает, что сходится ряд  , т. е. при |z|<|| исходный степенной ряд (1) сходится абсолютно.
, т. е. при |z|<|| исходный степенной ряд (1) сходится абсолютно.
Если же zрассматривать только из замкнутого круга  , то
, то  , а это означает, что степенной ряд (1) мажорируется сходящимся числовым рядом
, а это означает, что степенной ряд (1) мажорируется сходящимся числовым рядом  и по признаку Вейерштрасса исходный степенной ряд (1) сходится равномерно в круге
и по признаку Вейерштрасса исходный степенной ряд (1) сходится равномерно в круге 
Пусть теперь ряд (1) расходится в точке  . Предположим, что в точке
. Предположим, что в точке 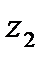 такой, что |
такой, что | 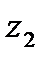 |>|
|>|  | ряд (1) сходится. Тогда по предыдущему утверждению ряд (1) сходится и в точке
| ряд (1) сходится. Тогда по предыдущему утверждению ряд (1) сходится и в точке  , что противоречит условию. Итак, для всех z таких, что |z|>|
, что противоречит условию. Итак, для всех z таких, что |z|>|  | ряд (1) расходится. [Теорема доказана]
| ряд (1) расходится. [Теорема доказана]
Параметры и радиус сходимости
Сходимость:пусть есть ряда1+а2+…+аn+… Егочастичныесуммы: S1=a1, S2=a1+a2 , …,Sn= a1 +….+ an .Ряд сходится if  , где S конечно.
, где S конечно.
Из теоремы Абеля можно сделать заключение о характере области сходимости степенного ряда. Точка z=0 всегда лежит в области сходимости ряда (1). Если область сходимости отлична от одной точки z=0 и от всей плоскости (z), то существует круг радиуса R, называемый кругом сходимости степенного ряда(1), в каждой точке которого ряд (1) сходится абсолютно, а вне точек круга расходится.
Для определения радиуса круга сходимости используется либо признак Даламбера, либо признак Коши.
Для каждого фиксированного zрассмотрим числовой ряд  (3) и применим к нему признак Даламбера. Именно: если существует предел
(3) и применим к нему признак Даламбера. Именно: если существует предел  (4) , то ряд (3) сходится, если
(4) , то ряд (3) сходится, если  и расходится, если
и расходится, если  . Отсюда заключаем, что если выполнено соотношение
. Отсюда заключаем, что если выполнено соотношение  , то ряд (3) сходится абсолютно, а если имеет место неравенство
, то ряд (3) сходится абсолютно, а если имеет место неравенство  , то ряд (1) как и ряд (3), расходится.
, то ряд (1) как и ряд (3), расходится.
Т.о., для определения радиуса круга сходимости степенного ряда получаем формулу  (5).
(5).
Если же к ряду (3) применим признак Коши то получим равенство
 из которого заключаем, что ряд (3) сходится, если
из которого заключаем, что ряд (3) сходится, если  , и расходится, если
, и расходится, если  . Т.о., радиус круга сходимости Rряда (1) определяется по формуле
. Т.о., радиус круга сходимости Rряда (1) определяется по формуле  . (6) (формула Коши — Адамара.)
. (6) (формула Коши — Адамара.)
Радиус сходимости степенного ряда - Rcx=  =
= 
Критерий равномерной сходимости.
Для того, чтобы функциональный ряд(в частности степенной ряд) сходился равномерно в области D, необходимо и достаточно, чтобы  и
и 
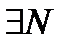 : при n>N
: при n>N
 , p =0,1,2,3,…
, p =0,1,2,3,…
Абсолютная сходимость: ряд а1+а2+…+аn+… сходится абсолютно, если сходится ряд |а1 |+|а2 |+…+|аn|+…
Непрерывность суммы
Свойство степенных рядов. Сумма степенного ряда есть функция, непрерывная на интервале сходимости ряда. S(z) = z0 + a1z + a2z2 + … + anzn + …
Причём, в том конце интервала, где степенной ряд сходится, его сумма S(x) остаётся односторонне непрерывной.
Почленная дифференцируемость
Теорема1:. Cтепенной ряд внутри интервала сходимости (|z|<R) имеет сумму S(x), к-я дифференцируема сколь угодно много раз. Степенной рядможно почленно дифференцировать любое число раз, причем радиус круга сходимости продифференцированных рядов также равен R.
S(x)= с0 + с1(z – z0) + с2(z – z0)2 + … + сn(z – z0)n + …
S’(x)= с1 + с2 *2*(z – z0) + … + сn*n*(z – z0)n-1 + …
Ряд Тейлора
Имеем степенной ряд  . Обозначим через f(z) его сумму. Сходится в круге |z -
. Обозначим через f(z) его сумму. Сходится в круге |z -  |<R.
|<R.
 называется рядом Тейлора функции f(z) по степеням (z-
называется рядом Тейлора функции f(z) по степеням (z-  ). Из почленной дифференцируемости имеем, что радиус сходимости тот же.
). Из почленной дифференцируемости имеем, что радиус сходимости тот же.
 - эти выражения называются коэффициентами Тейлора функции f(z) в точке
- эти выражения называются коэффициентами Тейлора функции f(z) в точке  . В случае
. В случае  =0 этот ряд называется также рядом Маклорена функции f(z).
=0 этот ряд называется также рядом Маклорена функции f(z).
4. Первообразная и неопределённый интеграл. Определение первообразной. Определение неопределённого интеграла, его свойства. Определение интеграла по Риману. Необходимые и достаточные свойства интегрируемости. Формула Ньютона-Лейбница.
Пусть определены функции f(x) и F(x). F(x) – первообразная f(x), если F’(x) = f(x). F(x) + c – тоже первообразная f(x).
Неопределенный интеграл:  - множество всех первообразных f(x).
- множество всех первообразных f(x).
Свойства неопределенного интеграла:
1) 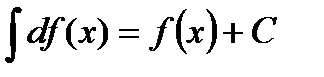
2) d 
3) 
4) 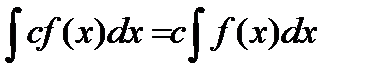 , где с – const
, где с – const
Определение интеграла по Риману
Пусть функция y=f(x) определена на отрезке [a; b], a<b. Выполним следующие действия:
1. С помощью точек  =a,
=a,  ,
,  ,…,
,…, 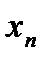 =b (
=b (  <
< 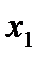 <
< 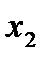 <…<
<…<  ) разобьем отрезок [a; b] на n частичных отрезков [
) разобьем отрезок [a; b] на n частичных отрезков [  ,
,  ], [
], [  ,
,  ],…, [
],…, [  ,
, 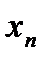 ]
]
2. В каждом частичном отрезке [  ,
,  ], i=1, 2,…, n выберем произвольную точку c
], i=1, 2,…, n выберем произвольную точку c  и вычислим значение функции в ней, т. е. величину
и вычислим значение функции в ней, т. е. величину  .
.
3. Умножим найденное значение функции  на длину
на длину  соответствующего частичного отрезка:
соответствующего частичного отрезка:  *
*  .
.
4.Сост. сумму S  всех таких произведений.:
всех таких произведений.:
 (1)
(1)
Сумма вида (1) называется интегральной суммой функции y=f(x) на отрезке [a; b]. Обозначим через  длину наибольшего частичного отрезка
длину наибольшего частичного отрезка 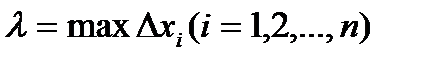 .
.
5. Найдем предел интегральной суммы (1), когда n  так, что
так, что  .
.
Если при этом интегральная сумма  имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции y=f(x) на отрезке [a,b]
имеет предел I, который не зависит ни от способа разбиения отрезка [a; b] на частичные отрезки, ни от выбора точек в них, то число I называется определенным интегралом от функции y=f(x) на отрезке [a,b] 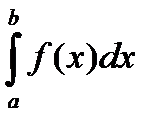 Т.о.,
Т.о.,  =
=  (2)
(2)
Необходимые и достаточные условия интегрируемости
Введём понятие верхней и нижней суммы Дабру. Пусть функция f(x) определена на отрезке [a; b], 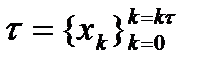 разбиение этого отрезка
разбиение этого отрезка 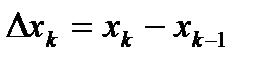 . Положим
. Положим  (т.е. Mk максимальное значение функции на отрезке [k-1;k]), m
(т.е. Mk максимальное значение функции на отрезке [k-1;k]), m 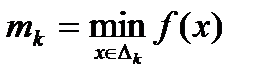 (mk - минимальное), k=1, 2,…, k
(mk - минимальное), k=1, 2,…, k  (3)
(3)
S  = S
= S  (f)=
(f)=  , s
, s  = s
= s  (f)=
(f)=  . (4)
. (4)
Сумма S  называется верхней, а сумма s
называется верхней, а сумма s 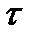 - нижней суммой Дарбу функции f. В случае, когда функция f ограничена, то нижние
- нижней суммой Дарбу функции f. В случае, когда функция f ограничена, то нижние  и верхние
и верхние  грани (3) конечны, и потому суммы Дарбу (4) при любом разбиении принимают конечные значения.
грани (3) конечны, и потому суммы Дарбу (4) при любом разбиении принимают конечные значения.
Теорема. Для того чтобы ограниченная на некотором отрезке функция была интегрируема на нем, необходимо и достаточно, чтобы суммы Дарбу S  и s
и s 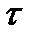 этой функции удовлетворяли условию
этой функции удовлетворяли условию  (5)
(5)
Следствие. Для того чтобы ограниченная на отрезке [a; b] функция f была на нем интегрируема, необходимо и достаточно, чтобы 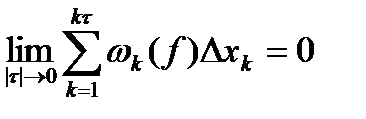 (6)
(6)
где  - разбиение отрезка [a; b], а
- разбиение отрезка [a; b], а  - колебание функции f на отрезке
- колебание функции f на отрезке  , k=1, 2,…, k
, k=1, 2,…, k  .
.
Формула Ньютона-Лейбница
Пусть функция y=f(x) интегрируема на отрезке [a; b].
Теорема.Если функция y=f(x) непрерывна на отрезке [a; b] и F(x) - какая-либо ее первообразная на [a; b] (F’(x)=f(x)), то имеет место формула 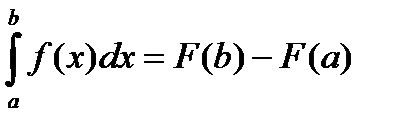
Доказательство:
Пусть на отрезке [a;b] задана интегрируемая функция f(x). Зададим произвольное значение  . Пусть функция F(x)- какая-нибудь первообразная для заданной функции f(x). Тогда она может быть получена по формуле
. Пусть функция F(x)- какая-нибудь первообразная для заданной функции f(x). Тогда она может быть получена по формуле  .Таким образом, учитывая, что C=F(a), имеем:
.Таким образом, учитывая, что C=F(a), имеем:  . Пологая теперь x=b получаем:
. Пологая теперь x=b получаем:  . Откуда:
. Откуда: 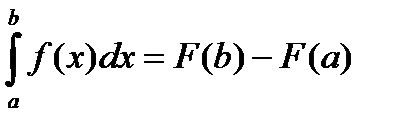
5. Основные понятия теории вероятности: классификация событий. Классические определения вероятности. Геометрические определения вероятности. Теоретико-множественная трактовка основных понятий и аксиоматическое построение теории вероятности.
Теорией вероятности наз. мат. наука, изучающая закономерности в случайных событиях.
Классификация событий:
Событие– всякий факт, который может произойти в результате некоторого опыта.
Достоверным называется событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий. Его вероятность равна 1 (P=1).
Невозможнымназывают событие, которое заведомо не произойдет, если будет осуществлена совокупность условий. Его вероятность равна 0 (P=0).
Случайное событие – такое событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти (0<P<1).
Два события называются совместными, если появление одного из них не исключает появления другого.
Два события называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.
Противоположные события –событие А называют противоположным B, если результат его противоположен результату B. P(A) + P(B) =1
Классическое определение вероятности: вероятность есть число, характеризующее степень возможности появления события. Каждый возможный результат – элементарный исход. Те элементарные исходы, в кот.интересующее нас событие наступает, называются благоприятствующими исходами. Т.о., событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих А. Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. P(A)=  , m – число элементарных исходов, благоприятствующих А;
, m – число элементарных исходов, благоприятствующих А;
n – число всех возможных элементарных исходов.
Недостаток классического определения вероятности – оно неприменимо к испытаниям с бесконечным числом исходов. Для преодоления этого недостатка вводят геометрические вероятности – вероятности попадания точки в область (отрезок, часть плоскости и т. д.).
Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Вероятность попадания точки на отрезок l определяется равенством:
P=  .
.
Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Вероятность попадания точки в фигуру g определяется равенством:
P=  .
.
Аксиоматическое построение теории вероятности.
Введем поле J элементарных событий, т.е. множество событий для к-х определены вероятности.  -пространство элементарных событий. J
-пространство элементарных событий. J  .
.
Аксиомы:
1) любому  соответствует некоторое неотрицательное число P(A) (вероятность этого события), причем P(A) может быть - 0<=P(A)<=1;
соответствует некоторое неотрицательное число P(A) (вероятность этого события), причем P(A) может быть - 0<=P(A)<=1;
2) P(  ) = 1 – достоверное событие;
) = 1 – достоверное событие;
3) Аксиома сложения вероятностей: Вероятность объединения несовместных событий равна сумме их вероятностей.
Объединением нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.
Теорема сложения вероятностей.
Вероятность появления 1 из 2 несовместных событий равна сумме вероятностей этих событий. P(A+B)=P(A)+P(B);m  -A, m
-A, m  -B. m
-B. m  + m
+ m  - число благопр. исходов или A или B.
- число благопр. исходов или A или B.
P(A+B)=  =
=  +
+ 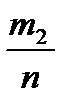 =P(A)+P(B).(из классического определения вероятности)
=P(A)+P(B).(из классического определения вероятности)
Вероятность появления одного из нескольких попарно-несовместных событий равна сумме вероятностей этих событий. P(A  +A
+A  +…+A
+…+A  )=P(A
)=P(A  )+P(A
)+P(A  )+…+P(A
)+…+P(A  ).
).
Сумма вероятностей A  , A
, A  ,…, A
,…, A  , образующих полную группу несовместных событий, всегда равна 1.
, образующих полную группу несовместных событий, всегда равна 1.
События называются полной группой if 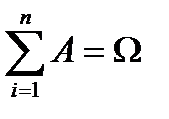 .
.
Условная вероятность. Вероятность наступления события А, зависящего от наступления события B называется условной вероятностью - P(A|B) =  (P(B)
(P(B)  0). Если события независимы (P(A|B)=P(A), P(B|A)=P(B)), то их вероятности безусловные.
0). Если события независимы (P(A|B)=P(A), P(B|A)=P(B)), то их вероятности безусловные.
Теорема умножения вероятностей.
Произведение событий. (A*B) – совместное появление этих событий.
Вероятность совместного появления 2 событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную, предположив, что первое событие уже наступило. P(A*B)=P(A)*P (B|A) = P(B)*P(A|B). Для независимых событий P(A*B)=P(A)*P(B).
Вероятность появления нескольких событий равна произведению вероятности одного из них на условную вероятность всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
P(A  , A
, A  ,…,A
,…,A  )=P(A
)=P(A  )*P (A
)*P (A  |A1)+…+P (A
|A1)+…+P (A  |A1A2….An-1).
|A1A2….An-1).
6. Случайная величина. Законы распределения случайной величины. Математическое ожидание и дисперсия случайной величины: определение, свойства. Вычисление математических ожиданий и дисперсий распределений: биноминального, Пуассона, нормального.
Случайной называется величина, которая в результате опыта может принять то или иное значение (только одно), причем до опыта неизвестно, какое именно. Пространство её значений – вероятностное пространство С.В(случайной величины). Существуют 3 типа С.В.: дискретные, непрерывные, непрерывно-дискретные. Дискретной случайной величиной называется такая величина, число возможных значений которой либо конечное, либо бесконечное (счетное множество). Непрерывной - возможные значения к-й непрерывно заполняют некоторый интервал на числовой оси. Непрерывно-дискретная – С.В, значения к-й непрерывно заполняют отдельные интервалы на числовой оси.
Так же С.В. могут быть классифицированы:
a)скалярные(X), векторные(X1,X2,…,Xn).
б)действительные, комплексные.
Закон распределения дискретной С.В..
P  =P(X=x
=P(X=x  ); P
); P  =P(X=x
=P(X=x  ); …; P
); …; P  =P(X=x
=P(X=x  ).
).
Сумма вероятностей всех значений равна 1. Законом распределения С.В. называется любое правило (таблица, функция), устанавливающее связь между возможными значениями С.В.(X) и соответствующими вероятностями. Для непрерывной С.В. – правило, функция. (табл. быть соответственно не может в силу непрерывности). Законы – F(x), f(x).
Функция распределения вероятности. F(x)
Функцией распределения С.В. X называется вероятность того, что она примет значения, меньшие, чем x: F(x)=P(X<x).
Свойства функции распределения.
1) Функция распределения есть неубывающая функция своего аргумента. x  >x
>x  , F(x
, F(x  )>F(x
)>F(x  ).
).
2) F(-  )=0.
)=0.
3) F(+  )=1.
)=1.
4) Функция распределения есть неотрицательная функция 0<=F(x)<=1.
5) Вероятность появления случайной величины в интервале (  ;
; 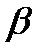 ) равна разности значений функции распределения в концах интервалов. P(
) равна разности значений функции распределения в концах интервалов. P(  <=x<=
<=x<= 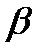 )=F(
)=F(  ) - F(
) - F( 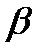 ).
).
6) Непрерывна слева
7) Функция распределения дискретной С.В. разрывна и возрастает скачками. (графически выглядит как лестница)
8)Непрерывна для непрерывной С.В.
Плотность распределения вероятности. f(x)
Плотность характеризует распределение только непрерывной С.В.. Будем считать С.В. непрерывной, если ее функция распределения дифференцируема. P(x<X<x+  x) = F(x+
x) = F(x+  x) – F(x).
x) – F(x).
 ;
; 
 =
= 
 =F’(x).
=F’(x).
f(x) = F’(x).
Плотность распределения С.В.– производная ее функции в данной точке. Плотность указывает на то, как часто появляется С.В. X в некоторой окрестности точки x при повторении опытов.
Св-ва: 1)F(x) =  2)F(+
2)F(+  ) =1
) =1 

3)f(x)  0 4) P(a<X<b) =
0 4) P(a<X<b) = 
Числовые характеристики С.В..
Мат. ожиданиемдискретной С.В. называют сумму произведений всех ее возможных значений на их вероятности.
Пусть X принимает значения x  , x
, x  ,…, x
,…, x  , вероятности к-х соответственно равны p
, вероятности к-х соответственно равны p  , p
, p  ,…, p
,…, p  .
.
M(X)=x  p
p  + x
+ x  p
p  +…+ x
+…+ x  p
p  =
=  .
.
Мат.ожидание непрерывной С.В.
Пусть непрерывная С.В X задана плотностью распределения f(x). Допустим, что все возможные значения X принадлежат отрезку [a; b]. Разобьем этот отрезок на n частичных отрезков длиной  ,
,  ,…,
,…,  и выберем в каждом из них произвольную точку x
и выберем в каждом из них произвольную точку x  (i=1, 2,…, n). Определим мат. ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x
(i=1, 2,…, n). Определим мат. ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений x  на вероятности попадания их в интервал
на вероятности попадания их в интервал  :
:  .
.
Перейдем к пределу: 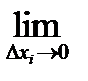
 =
=  ; M(X)=
; M(X)=  .
.
Свойства математического ожидания:
1. Мат. ожидание постоянной величины равно самой постоянной M(C)=C.
2. Постоянный множитель можно выносить за знак мат.ожидания M(CX)=CM(X).
3. Мат.ожидание произведения двух независимых С.В. равно произведению их мат.ожиданий M(XY)=M(X)M(Y).
4. Мат.ожидание суммы двух С.В. равно сумме мат. ожиданий слагаемых M(X+Y)=M(X)+M(Y).
Дисперсиейдискретной С.В. называют мат.ожидание квадрата отклонения случайной величины от ее мат. ожидания: D(X)=M[X-M(X)]  .
.
По определению дисперсии:
D(X)=M[X-M(X)]  =[x
=[x  -M(X)]
-M(X)]  p
p  +[x
+[x  -M(X)]
-M(X)]  p
p  +…+[x
+…+[x  -M(X)]
-M(X)]  p
p  .
.
Дисперсия равна разности между мат. ожиданием квадрата С.В. X и квадратом ее мат. ожидания. D(X)=M(X  )-[M(X)]
)-[M(X)]  .
.
D(X)=M[X-M(X)]  =M[X
=M[X  -2XM(X)+M
-2XM(X)+M  (X)]= M(X
(X)]= M(X  )-2M(X)M(X)+ M
)-2M(X)M(X)+ M  (X)= =M(X
(X)= =M(X  )-2M
)-2M  (X)+M
(X)+M  (X)= M(X
(X)= M(X  )- M
)- M  (X)= M(X
(X)= M(X  )-[M(X)]
)-[M(X)]  .
.
Дисперсией непрерывной случайной величины называют мат.ожидание квадрата ее отклонения. Если возможные значения X принадлежат отрезку [a; b], то D(X)= 
(a и b могут быть 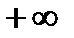 и -
и -  соответственно)
соответственно)
Свойства дисперсии:
1. Дисперсия постоянной величины C равна 0 D(C)=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат D(CX)= C  D(X).
D(X).
3. Дисперсия суммы(разности) двух независимых С.В. равна сумме(разности) дисперсий этих величин D(X  Y)=D(X)
Y)=D(X) 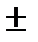 D(Y).
D(Y).
4. D(X)=M(X  )-[M(X)]
)-[M(X)]  .
.
D(X)=M[X-M(X)]  =M[X
=M[X  -2XM(X)+M
-2XM(X)+M  (X)]= M(X
(X)]= M(X  )-2M(X)M(X)+ M
)-2M(X)M(X)+ M  (X)= =M(X
(X)= =M(X  )-2M
)-2M  (X)+M
(X)+M  (X)= M(X
(X)= M(X  )- M
)- M  (X)= M(X
(X)= M(X  )-[M(X)]
)-[M(X)]  .
.
Вычисление мат.ожидания и дисперсии при биномиальном распределении.
X 
| … | n | |||
p 
| p 
| p 
| p 
| … | p 
|
– число появления события A в n независимых опытах. P(A)=p; q=1-p; X{0, 1, 2,…, n},
/////////////////////на всякий случай вывод для тех, кому очень интересно
Формула распределения:
P (m) = 
По определению, математическое ожидание случайной величины вычисляется по формуле:
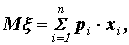
где
x i - значения случайной величины x ,
p i - вероятности событий  .
.
Для закона распределения случайной величины мы получим:

Поскольку
 ,
,
то

Окончательно:

Для дисперсии, по определению, имеем:
 .
.
получим:

///////////////////////////////////////////////////////////////
p  (k)=C
(k)=C  p
p  q
q 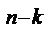 . M(x)=np. D(x)=npq.
. M(x)=np. D(x)=npq.
Вычисление мат. ожидания и дисперсии при распределении Пуассона.
X – число появлений события A в n независимых испытаниях.
///////////////////////////////////////////////////////////// на всякий случай вывод для тех, кому очень интересно
Рассмотрим второй случай асимптотического приближения биномиального распределения, когда  , а
, а  – имеет конечное значение. Случайная величина
– имеет конечное значение. Случайная величина  называется распределенной по закону Пуассона с параметром
называется распределенной по закону Пуассона с параметром  , если эта случайная величина может принимать значения
, если эта случайная величина может принимать значения  , соответствующая вероятность которых определяется по формуле Пуассона, когда
, соответствующая вероятность которых определяется по формуле Пуассона, когда  :
:
 .
.
В биномиальном распределении величина  имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона:
имеет смысл математического ожидания. Проведем вычисления математического ожидания для распределения Пуассона:
 .
.
Таким образом, в распределении Пуассона величина  также имеет смысл математического ожидания.
также имеет смысл математического ожидания.
Проведем вычисления дисперсии для распределения Пуассона:


 ,
,
поскольку
 ,
,

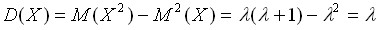
Таким образом, в распределении Пуассона дисперсия также равна 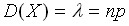
///////////////////////////////////////////////////////////
P  (k)=
(k)=  ;
;  – параметр распределения;
– параметр распределения;  =np; M(x)= D(X)=
=np; M(x)= D(X)=  .
.
Вычисление мат.ожидания и дисперсии при нормальном законе распределения.
Нормальным называют распределение вероятностей непрерывной С.В., которое описывается плотностью f(x)=  .
.
Нормальное распределение определяется двумя параметрами: a и  . Достаточно знать эти параметры, чтобы задать нормальное распределение.
. Достаточно знать эти параметры, чтобы задать нормальное распределение.
M(X)=a. D(X)= 
 .
.
7. Законы больших чисел и предельные теоремы: неравенство Маркова, неравенство Чебышева, теорема Чебышева, центральная предельная теорема.
Законы больших чисел и предельные теоремы
Закон больших чисел (в широком смысле) – общий принцип, согласно которому, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и м.б. предсказан с большой степенью определенности.
Закон больших чисел (в узком смысле) – ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенство Маркова (лемма Чебышева)
Теорема.Если случайная величина X принимает только неотрицательные значения и имеет мат. ожидание, то для любого положительного числа А верно неравенство P(x>A) 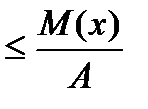 . (1)
. (1)
Доказательство: проведем для дискретной случайной величины X. Расположим ее значения в порядке возрастания, из которых часть значений x  , x
, x  ,…, x
,…, x  будут не более числаА, а другая часть - x
будут не более числаА, а другая часть - x  ,…, x
,…, x  будут больше А, т.е.x
будут больше А, т.е.x  <=A, x
<=A, x  <=A,…, x
<=A,…, x  <=A; x
<=A; x  >A,…, x
>A,…, x  >A.
>A.
Запишем выражение для математического ожидания M(X):
x  p
p  + x
+ x  p
p  +…+ x
+…+ x  p
p  + x
+ x  p
p  +…+ x
+…+ x  p
p  =M(X)
=M(X)
где p  , p
, p  ,…, p
,…, p  - вероятности того, что случайная величина Х примет значения соответственно x
- вероятности того, что случайная величина Х примет значения соответственно x  , x
, x  ,…, x
,…, x  .
.
Отбрасывая первые k неотриц. слагаемых получим x  p
p  +…+ x
+…+ x  p
p  <=M(X) (2)
<=M(X) (2)
Заменяя в неравенстве (2) значения x  ,…, x
,…, x  меньшим числомА, получим более сильное неравенство A(p
меньшим числомА, получим более сильное неравенство A(p  +…+ p
+…+ p  )<=M(X) или p
)<=M(X) или p  +…+ p
+…+ p  <=
<=  .
.
Сумма вероятностей в левой части полученного неравенства представляет собой, сумму вероятностей событий X=x  ,…X=x
,…X=x  т.е. вероятность события X>A.
т.е. вероятность события X>A.
Поэтому P(X>A) <=  .
.
Неравенство Чебышева
Теорема.Для любой случайной величины, имеющей мат. ожидание и дисперсию, справедливо неравенство Чебышева: P(|X-a|>  )<=
)<= 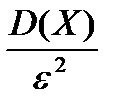 , (3) где a=M(X),
, (3) где a=M(X),  >0. ( P(|X-a|
>0. ( P(|X-a| 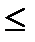
 )
)  1 -
1 - 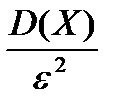 - другая форма записи неравенства Чебышева, тоже правильная.Ее давал Герман)
- другая форма записи неравенства Чебышева, тоже правильная.Ее давал Герман)
Доказательство: Применим неравенство Маркова в форме (1) к случайной величине X’=(X-a)  взяв в качестве положительного числа A=
взяв в качестве положительного числа A=  . Получим
. Получим  <=
<=  . (4)
. (4)
Т.к. неравенство  равносильно неравенству |X-a|>
равносильно неравенству |X-a|>  , а M(X-a)
, а M(X-a)  есть дисперсия случайной величины X, то из неравенства (4) получаем доказываемое неравенство (3).
есть дисперсия случайной величины X, то из неравенства (4) получаем доказываемое неравенство (3).
Теорема Чебышева
Если дисперсии n независимых С.В. X  , X
, X  ,…, X
,…, X  ограничены одной и той же постоянной, топри неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их мат. ожиданий (M (x1) = a
ограничены одной и той же постоянной, топри неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их мат. ожиданий (M (x1) = a  , M (x2) = a
, M (x2) = a  ,…, a
,…, a  =M (xn), т. е.
=M (xn), т. е.
 (5) или
(5) или  .
.
Докажем формулу (5). По условию M(X  )=a
)=a  , M(X
, M(X  )=a
)=a  ,…, M(X
,…, M(X  )=a
)=a  ,
,
Возьмем такое С: D(X  )<=C, D(X
)<=C, D(X  )<=C,…, D(X
)<=C,…, D(X  )<=C, где C - постоянное число.
)<=C, где C - постоянное число.
Получим неравенство Чебышева для средней арифметической случайных величин, т.е. для X=  . Найдем мат. ожидание M(X) и оценку дисперсии D(X)
. Найдем мат. ожидание M(X) и оценку дисперсии D(X)
M(X)=M(  )=
)=  ;
;
D(X)=D(  )=
)= 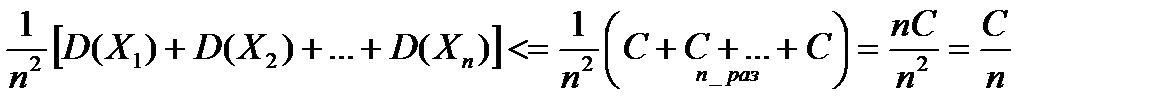 .
.
(Здесь использованы свойства математического ожидания и дисперсии, в частности, то, что случайные величины X  , X
, X  ,…, X
,…, X  независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)
независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)
Применяем неравенство Чебышева(вариант Германа) для С.В - X=(X  ,X
,X  ,…,X
,…,X  )/n;
)/n;  (6)
(6)
Т.к. по доказанному D(X) 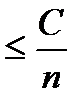 , то 1-
, то 1- 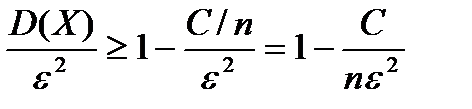 , и от неравенства (6) перейдем к более сильному неравенству:
, и от неравенства (6) перейдем к более сильному неравенству:  (7)
(7)
В пределе при n  величина
величина  стремится к нулю, и получим доказываемую формулу (5).
стремится к нулю, и получим доказываемую формулу (5).
Центральная предельная теорема
Рассмотрим другую закономерность, возникающую в результате суммарного действия случайных величин. При некоторых условиях совокупное действие случайных величин приводит к определенному, а именно — к нормальному закону распределения.Центральная предельная теорема представляет собой группу теорем, посвященных установлению условий, при которых возникает нормальный закон распределения. Среди этих теорем важнейшее место принадлежит теореме Ляпунова.
Теорема Ляпунова. Если .X  , X
, X  ,…, X
,…, X  независимые С.В, у каждой из к-х существует мат. ожидание M(X
независимые С.В, у каждой из к-х существует мат. ожидание M(X  )=a, дисперсия D(X
)=a, дисперсия D(X  )=
)=  , абсолютный центральный момент третьего порядка M(|X
, абсолютный центральный момент третьего порядка M(|X  -a
-a  |
|  )=m
)=m  и
и  . (80) , то закон распределения суммы Y
. (80) , то закон распределения суммы Y  =X
=X  +X
+X  +…+X
+…+X  при n
при n  неограниченно приближается к нормальному с математическим ожиданием
неограниченно приближается к нормальному с математическим ожиданием  и дисперсией
и дисперсией  .
.
В данном вопросе громоздкие, хотя и достаточно понятные доказательства теорем без к-х ответ окажется очень маленьким. Хотя по усмотрению, можете обойтись перечислением теорем если не успеваете.
8.Проверка статистических гипотез: принципы практической уверенности, статистическая гипотеза и общая схема её проверки, основная и альтернативная гипотезы, простая и сложные гипотезы, ошибки первого и второго ряда при проверке гипотезы, мощность критерия
Пусть имеется некоторая выборка  значений случайной величины
значений случайной величины  , функция распределения которой неизвестна. Статистической гипотезой
, функция распределения которой неизвестна. Статистической гипотезой  называется любое предположение о распределении наблюдений, например, предположение о том, что функция распределения
называется любое предположение о распределении наблюдений, например, предположение о том, что функция распределения  совпадает с некоторой наперед заданной функцией
совпадает с некоторой наперед заданной функцией  :
:  (такая гипотеза называется простой), или о том, что функция распределения принадлежит некоторому параметрическому семейству распределений
(такая гипотеза называется простой), или о том, что функция распределения принадлежит некоторому параметрическому семейству распределений  :
:  (сложная статистическая гипотеза).
(сложная статистическая гипотеза).
Если рассматривается всего 2 взаимоисключающие гипотезы, то одну из них принято называть основной (нулевой) и обозначать  , а другую – альтернативной (противоположной), она обозначается
, а другую – альтернативной (противоположной), она обозначается  . Обычно за
. Обычно за  принимается такая гипотеза, отвержение которой, когда она на самом деле верна, будет иметь наихудшие последствия по сравнению с теми, когда за
принимается такая гипотеза, отвержение которой, когда она на самом деле верна, будет иметь наихудшие последствия по сравнению с теми, когда за 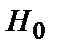 выбирается другая гипотеза.
выбирается другая гипотеза.
При проверке статистических гипотез используется принцип практической уверенности: «если вероятность события А в данном опыте весьма мала, то можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление; если же вероятность события близка к 1, то можно предполагать, что оно достоверно произойдет». Таким образом, при правильном выборе допустимого отклонения вероятности правильного решения о принятии или не принятии гипотезы мы можем на основании вероятностных данных делать выводы невероятностного характера (например, о свойствах случайных величин).
Типовые постановки задачи при проверке статистических гипотез:
1)
Дата добавления: 2015-04-18; просмотров: 415; Мы поможем в написании вашей работы!; Нарушение авторских прав