Если функция непрерывна на отрезке, то она ограничена на нем.

2. Теорема Вейерштрасса:

Пусть f(x) непрерывна на отрезке [a;b]. Тогда

Следствие: если функция непрерывна на отрезке, то она достигает наибольшего и наименьшего значения на нем.

3. Теорема Больцано-Коши:

Пустьf(x) непрерывнанаотрезке [a;b], f(a) = A, f(b) = B, A B.

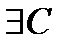
Тогда , A< <B [a; b] : .

Следствие: если функция непрерывна на отрезке, то она принимает все значения на нем.

Прим.: теорема не утверждает, что точка - единственная.

Непрерывность многочленной и рациональной функции:

Т.к. произведение непрерывных функций есть функция непрерывная, отсюда следует непрерывность любого одночленного выражения ax 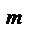= a* (ifF(x)=x непрерывная функция).

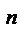Непрерывность многочлена (целой рациональной функции) a x + a x + … + a x + a следует из непрерывности суммы непрерывных функций. В этих случаях непрерывность имеет место во всем промежутке (- 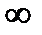; + ).(Сумма непрерывных функций есть непрерывная функция)

Частное двух многочленов (дробная рациональная функция)

также будет непрерывно при каждом значении x, кроме тех, которые обращают знаменатель в 0.

Терема о среднем для действительных функций одного действительного переменного. Теорема Ферма; теорема Ролля; теорема Лагранжа. Примеры показывающие существенность каждого условия в теореме Роля; геометрическая интерпретация.

Теорема о среднем – совокупность: Т. Ферма, Т. Роля, Т. Коши, Т. Лагранжа.

Теорема Ферма:

Пусть функция определена и непрерывна на промежутке [a;b]и в некоторой точке 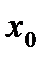этого промежутка достигает своего наибольшего и наименьшего значения, если в этой точке , то

Доказательство:

Пусть, для определенности, в точке функция достигает своего наибольшего. По условию теоремы эта точка внутренняя, т.е. a<x<b, и поэтому к этой точке можно подойти и справа и слева.

Пусть мы подходим к точке слева. Тогда ,т.к. 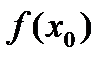-наибольшее значение.

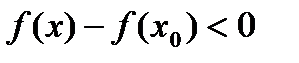, (т.к. подходим слева) =>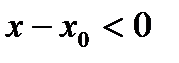

Делая предельный переход 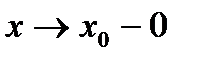получим 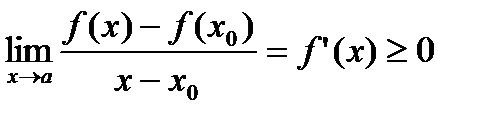(1)

Пусть мы подходим к точке справа. Тогда ,т.к. 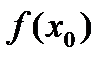-наибольшее значение.

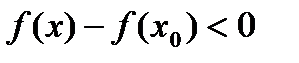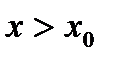, (т.к. подходим справа) =>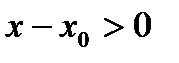

Делая предельный переход получим (2)

Сопоставляя соотношения (1) и (2), приходим к заключению, что

Аналогично для наименьшего значения.

Теорема Ролля:

Пусть:

1) функция f(x) определена и непрерывна на замкнутом промежутке [a; b];

2) ;

3) на концах промежутка функция принимает равные значения

Тогда :

Доказательство: f(x) непрерывна в замкнутом промежутке [a; b], поэтому

– по т.Вейрштрасса

x [a; b] m<= f(x) <= M.

Рассмотрим 2 случая:

1) M=m. Тогда f(x) в промежутке [a; b] сохраняет постоянное значение. Производная const равна 0.

2) (M>m).

Оба эти значения функцией достигаются, но, т.к. f(a) = f(b), то они не могут оба достигаться на концах промежутка и хоть одно из них достигается в некоторой точке между a и b (Если, к примеру, , тогда , т.е. не может быть равно а). Производная в этой точке обращается в 0 ( либо , либо 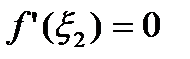- из т.Ферма). Теорема доказана.

Замечание: теорема Ролля не утверждает, что такая точка одна.

На геометрическом языке теорема Роля означает следующее: если крайние кординаты кривой y=f(x) равны, то на кривой найдется точка, где касательная параллельна оси x.

Примеры показывающие существенность условий - в доказательстве (без всех условий теорема не доказуема).

Теорема Лагранжа. Пусть:

1) f(x) определена и непрерывна на замкнутом промежутке [a; b],

2) f(x) дифференцируема на (a; b).

Тогда

Доказательство: Введем вспомогательную функцию F(x), определив ее в промежутке [a; b] равенством:

Эта функция непрерывна на [a; b], т.к. представляет собой разность между непрерывной функцией f(x) и линейной функцией. В промежутке (a; b) она имеет определенную конечную производную, равную

.

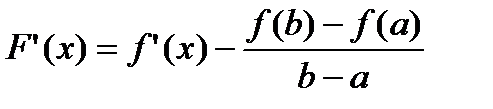Подстановкой можно убедиться, что F(a)=F(b)=0, т. е. F(x) принимает равные значения на концах промежутка. Следовательно, по теореме Ролля, на интервале (a; b) существует

, т. е Теорема доказана.