
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Криптосистемы на основе эллиптических кривых.
Разработка криптосистемы на эллиптических кривых заключается в выборе поля, уравнения эллиптической кривой и числа точек.
Пусть E(Fq)-эллиптическая кривая над полем из q=pn элементов, QϵE(Fq) и #‹Q›=r.
Для достижения максимального уровня стойкости криптосистемы, равного O(  ), эллиптическая кривая должна удовлетворять следующим требованиям:
), эллиптическая кривая должна удовлетворять следующим требованиям:
1. Для обеспечения стойкости к анализу методом Гельфонда порядок r циклической группы должен быть простым большим числом (для задач аутентификации достаточно 200-250 бит, для шифрования долговременных секретов достаточно 400-500 бит).
2. Для обеспечения стойкости к анализу на основе спаривания Вейля порядок r группы не должен быть делителем ни одного из чисел q-1,q2-1,…,qm-1. Практически для задач аутентификации достаточно проверить это для m=100.
3. Для обеспечения стойкости к анализу методом логарифмической производной должно выполняться равенство r ≠ p.
Кроме того, выбранная эллиптическая кривая должна обеспечивать высокую скорость вычислений. Это достигается соответствующим выбором характеристики поля, выбором полинома, а также выбором кривой, допускающей комплексное умножение или иной способ быстрого умножения точки на число.
Операция сложения точек в криптографии на основе эллиптических кривых является аналогом операции умножения чисел по модулю простого числа, а многократное повторное сложение точек — аналогом возведения числа в степень. Чтобы построить криптографическую систему, используя эллиптические кривые, нужно найти «трудную проблему», соответствующую разложению на множители произведения двух простых чисел или дискретному логарифмированию.
Рассмотрим уравнение 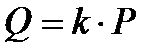 , где
, где 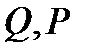 - точки на ЭК и
- точки на ЭК и  . Относительно легко вычислить
. Относительно легко вычислить  по данным
по данным  и
и  , но относительно трудно определить
, но относительно трудно определить  , имея
, имея 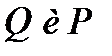 .
.
В общем случае кубические уравнение для эллиптических кривых имеет вид:

 , где
, где  – действительные числа. Определение эллиптической кривой включает также нулевой элемент
– действительные числа. Определение эллиптической кривой включает также нулевой элемент  (точка на бесконечности).
(точка на бесконечности).
Пусть  и
и 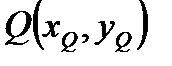 - точки на ЭК. Определим точки
- точки на ЭК. Определим точки  и
и  :
:
1.  Тогда
Тогда 

2.  если
если  Тогда
Тогда 
3. Если  то прямая
то прямая  имеет ещё одно пересечение с ЭК в точке
имеет ещё одно пересечение с ЭК в точке  . Тогда
. Тогда 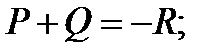 Исключение – если
Исключение – если  является касательной в точке
является касательной в точке  (
( 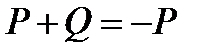 ) или в точке
) или в точке  (
(  ).
).
4.  Тогда
Тогда  - касательная к ЭК в точке
- касательная к ЭК в точке 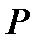 , которая имеет ещё одно пересечение с ЭК в точке
, которая имеет ещё одно пересечение с ЭК в точке  .
. 
Вышеприведенные правила сложения и множество точек ЭК образуют абелеву группу. Также 
Перейдём к редуцированной форме ЭК, которая определяется над конечным простым полем 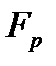 характеристики
характеристики 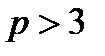 :
:
 , где
, где  - условие невырожденности точек кривой,
- условие невырожденности точек кривой, 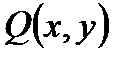 - точка на ЭК,
- точка на ЭК,  .
.
Определим правила сложения двух точек, используя правила, описанные выше: 


Дата добавления: 2015-04-18; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |