Связь энергии и импульса.

Обсудим теперь некоторые следствия из
полученных формул. Во первых, из определения
импульса (9.2) и энергии частицы (9.7) следует, что
импульс частицы связан с ее энергией
соотношением

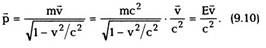
Из этой формулы следует, в частности, что,
если какая —либо частица может двигаться со
скоростью v = c, то ее импульс связан с энергией
по формуле

Далее, возводя (9.2) в квадрат и вычитая из
полученного выражения Е²/с² , получим

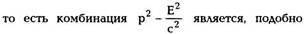
Второе слагаемое в (9.8) совпадает с
кинетической энергией частицы в классической
механике. Однако, при v = 0 энергия свободной
частицы (энергия покоя)

оказывается отличной от нуля. Таким образом,
СТО приводит к новому, весьма важному выводу:
всякая частица или тело, обладающее массой т.

обладает вместе с тем энергией покоя тс².
Естественно тогда определить кинетическую
энергию частицы в СТО, как

Это выражение переходит в классическое,
если скорость частицы v « с . На первый взгляд
может показаться, что определение энергии (9.7)
является произвольным. Поскольку энергия
найдена из дифференциального соотношения (9.6),
ее можно определить как

таким образом энергия при v«с будет
совпадать с кинетической энергией частицы в
классической механике. В действительности,
однако, легко показать, что константу следует
положить равной нулю, как это было сделано в
(9.7).

лекции), инвариантной относительно

преобразований Лоренца, так как справа в (9.12)
стоит масса частицы, одинаковая во всех ИСО.
Отсюда следует, что при переходе от системы К к
системе К' (или наоборот) компоненты импульса

x,y,z и t. Делая в (8.7) соответствующие замены,
получим: