
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
БИМАТРИЧНЫЕ ИГРЫ 2х2
Б И М А Т Р И Ч Н Ы Е И Г Р Ы
ОСНОВНЫЕ ПОНЯТИЯ И СИТУАЦИЯ РАВНОВЕСИЯ
В матричной игре интересы двух игроков были прямо противоположны, то есть речь шла об антагонистической игре. Однако гораздо чаще встречаются ситуации, в которых интересы игроков хотя и не совпадают, но не обязательно являются противоположным.
Рассмотрим конфликтную ситуацию, в которой два игрока имеют следующие возможности для выбора своей линии поведения:
а) 1-й игрок может выбрать любую из стратегий  ;
;
б) 2-й игрок - любую из стратегий  .
.
При этом, в ситуации  выигрыш первого игрока будет равен
выигрыш первого игрока будет равен  , а второго -
, а второго -  , причем, вообще говоря
, причем, вообще говоря  .
.
Тогда получаем две платежные матрицы размерности 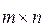 :
:
 и
и  . (3.1)
. (3.1)
Здесь  – платежная матрица 1-го игрока,
– платежная матрица 1-го игрока,  - платежная матрица 2-го игрока.
- платежная матрица 2-го игрока.
В этом случае говорят, что речь идет о биматричной игре двух игроков с платежными матрицами (1).
Отметим, что при  получаем обычную матричную игру.
получаем обычную матричную игру.
Рассмотрим один пример биматричной игры.
№ 3.1.(Преподаватель - Студент). Студент (1-й игрок) готовится к зачету, который принимает Преподаватель (2-й игрок). У студента есть две стратегии  - подготовиться к зачету,
- подготовиться к зачету,  - не готовиться. У преподавателя есть две стратегии:
- не готовиться. У преподавателя есть две стратегии: 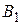 поставить зачет и
поставить зачет и 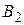 - не поставить зачет. Постройте платежные матрицы игры.
- не поставить зачет. Постройте платежные матрицы игры.
Решение. В основу значений функции выигрыша положим следующие качественные соображения:
| Выигрыш студента | Сдал зачет | Не сдал зачет |
| Готовился к зачету | оценка заслужена | очень обидно |
| Не готовился к зачету | удалось обмануть | оценка заслужена |
…
| Выигрыш преподавателя | Поставил зачет | Не поставил зачет |
| Готовился к зачету | все нормально | был не прав |
| Не готовился к зачету | дал себя обмануть | опять придет |
Количественно выигрыши игроков можно выразить, например, как
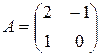 ,
,  .
.
Рассматривая биматричную игру, перейдем сразу к смешенным стратегиям и определим средние выигрыши игроков математическим ожиданием:
 ,
,  . (3.2)
. (3.2)
Будем говорить, что пара векторов  и
и  определяют равновесную ситуацию, если при любых
определяют равновесную ситуацию, если при любых  и
и  , удовлетворяющих условиям
, удовлетворяющих условиям  ,
, 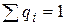 ,
,  , справедливы неравенства:
, справедливы неравенства:
 . (3.3)
. (3.3)
Неравенства (3.3) означают, что если игрок отклонится от равновесной ситуации  , то его выигрыш может только уменьшиться.
, то его выигрыш может только уменьшиться.
На вопрос о существовании ситуации равновесия отвечает следующая теорема.
Теорема 3.1. (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.
Остается разрешить проблему нахождения этой ситуации равновесия.
БИМАТРИЧНЫЕ ИГРЫ 2х2
Рассмотрим биматричную игру  :
:
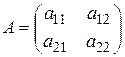 ,
,  ,
,
с вероятностями  ,
,  ,
, 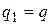 ,
,  .
.
Дата добавления: 2015-01-29; просмотров: 1481; Мы поможем в написании вашей работы!; Нарушение авторских прав |