Вычислим средние выигрыши игроков

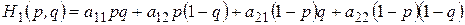, (3.4)

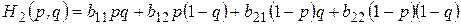(3.4’)

Для таких игр оказывается справедливой следующая теорема, позволяющая находить смешенные стратегии.

Теорема 3.2. Выполнение неравенств (3.3):

,

равносильно выполнению следующих неравенств:

(3.5)

Другими словами, чтобы убедиться в том, что пара определяет равновесную ситуацию достаточно проверить справедливость неравенств (3) не для всех и , а только для двух чистых стратегий каждого игрока.

Перепишем формулу (3.4) в более удобном виде

.

Положим здесь и :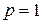

,

,

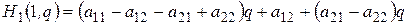и рассмотрим разности

,

.

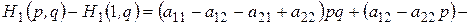
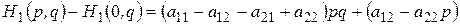Полагая

(3.6)

получим

,

.

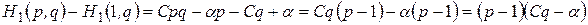Так как в точке равновесия эти разности должны быть неотрицательными, то приходим к следующей системе неравенств:

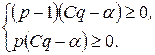
Для , при обозначениях:

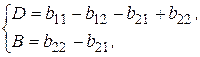(3.7)

получаем аналогичным образом:

Таким образом, для того, чтобы пара 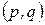определяла равновесную ситуацию в биматричной игре необходимо и достаточно справедливости системы неравенств:

(3.8)

где 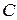, , , 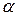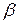вычисляются по формулам (6) - (7).