ПОИСК РАВНОВЕСНЫХ СИТУАЦИЙ

№ 3.2.Решите биматричную игру в условиях № 3.1.

Решение. Вычислим параметры системы (3.8):

,

.

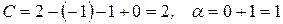Тогда получаем следующие системы неравенств:

и

Решим первую из систем:

. , , .

. , , .

. , .

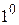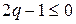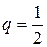Перенесём эти результаты на чертеж в виде «зигзага»:

Рис.3.1

Решим вторую систему:

. , , .

. , , .

. , , .

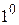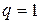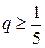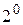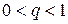Перенесём эти результаты на чертеж в виде «зигзага»:

Рис. 3.2

Объединим эти рисунки.

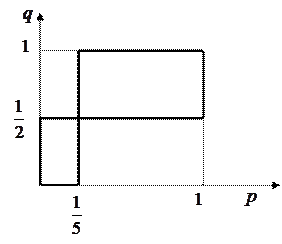Рис. 3.3

Видим, что игра имеет три равновесные ситуации с соответствующими выигрышами:

1) , , , .

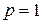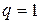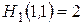2) , , , .

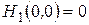3) , , , .

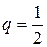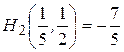Из этих трех смешанных стратегий, очевидно, лучшей является первая с 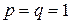, то есть хорошо подготовиться к зачету и поставить зачет.

В этом примере реализуется весьма редкая для биматричных игр ситуация, когда функции выигрышей игроков достигают максимума одновременно.

№ 3.3.«Борьба за рынки».

Небольшая фирма (1-й игрок) намерена сбыть партию товара на одном из двух рынков, монополизируемых другой, более крупной фирмой (2-ой игрок). Для этого фирма готова предпринять по одному из рынков соответствующие приготовления, например, развернуть рекламную кампанию. Фирма может воспрепятствовать этому, предприняв по одному из рынков предупредительные меры. Если фирма встречает противодействие, то терпит поражение, в противном случае – захватывает рынок.

Будем считать, что проникновение фирмы на 1-ый рынок более выгодно для нее, чем на второй, но и поражение на первом рынке принесет фирме большие, чем на втором рынке.

Таким образом, фирмы имеют по две стратегии:

и - выбор первого рынка,

и 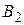- выбор второго рынка.

Составьте и решите биматричную игру.

Решение. Составим платежные матрицы игроков в условных единицах, исходя из соответствующих качественных соображений:

и .

Из этих матриц видно, что если обе фирмы выберут один рынок, то выигрывает фирма , если разные – то фирма .

Найдем равновесные ситуации, вычислив параметры системы (3.8):

, ,

, .

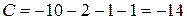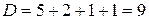Тогда получаем следующие системы неравенств:

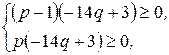
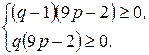
Решим эти системы неравенств:

1)

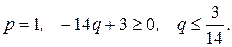
2)

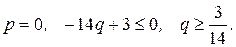
3)

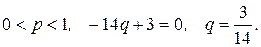
1)

2)

3)

4)

Изобразим эти решения на рисунке.

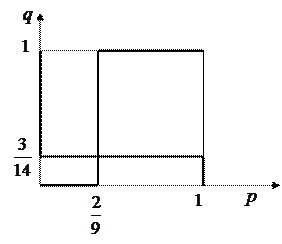Рис. 3.4

Видно, что получилась одна точка равновесия 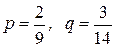. Это дает нам следующие оптимальные смешанные стратегии игроков:

,

которым соответствуют оптимальные (средние) выигрыши

, .

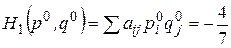Таким образом, если игра может быть повторена многократно в схожих условиях, то фирма примерно в 22% случаев должна осуществлять попытки проникновения на первый рынок, а в 78% - на второй рынок. При этом (в среднем) она не проиграет больше, чем у.е. Фирме рекомендуется в 21% случаев оказывать противодействие на первом рынке, а в 79% - на втором. В этом случае ее средний выигрыш составит не мене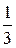е у.е.

Отметим, что в этой задаче получилась одна равновесная точка, и 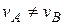. В других биматричных играх можно получить несколько равновесных ситуаций, как, например, в задаче «Преподаватель-Студент». В этом случае встает проблема выбора оптимальной в некотором смысле ситуации, из нескольких равновесных. Эту задачу можно попытаться решить исходя из содержательного смысла игры.

Из рассмотренных примеров видно, что точка равновесия определяется парой

. (3.9)

А это означает, что в равновесной ситуации выбор одного игрока полностью определяется платежной матрицей другого игрока, и не зависит от собственной платежной матрицы. Другими словами, равновесная ситуация определяется не столько стремлением увеличить свой выигрыш, сколько желанием держать под контролем выигрыш другого игрока.

Проиллюстрируем это на предыдущем примере. Для этого разобьем биматричную игру на две матричные игры с матрицами

и ,

и решим их:

,

.

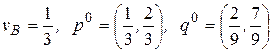То есть, если каждый игрок будет применять свои стратегии в биматричной игре, исходя только из собственной матрицы выигрышей, то он найдет свой оптимальный выигрыш и оптимальную стратегию другого игрока.

Таким образом, в биматричной игре вновь встречаемся с антагонизмом. Только это не антагонизм интересов, а антагонизм поведения.

Кроме того, в биматричных играх, при наличии нескольких равновесных ситуаций, средние выигрыши игроков разнятся, и встает вопрос о том. какой ситуации следует отдать предпочтение.

И последнее. Достаточно сложной является и проблема перехода от качественных оценок ситуаций к количественным оценкам. То есть, если, например, в задаче «Преподаватель-Студент» принять другие количественные оценки выигрышей, то можно получить и другие ситуации равновесия.