ПОНЯТИЕ ИГРЫ С ПРИРОДОЙ

Ситуации, рассмотренные в предыдущих главах, могут в экономической практике оказаться не вполне адекватными действительности, поскольку реализация моделей матричных игр предполагала возможность многократного повторения решений (действий), предпринимаемых в похожих условиях. На практике же количество экономических решений, принимаемых в похожих условиях, жестко ограничено. Нередко экономическая ситуация является уникальной, и решение должно приниматься однократно и в условиях неопределенности.

Неопределенность присутствовала и в рассмотренных выше антагонистических играх. Заключалась она в том, что ни один из игроков не обладал информацией о действиях противника. Но эта неопределенность в некоторой степени компенсировалась предположением о том, что игроки действуют осознанно, выбирая стратегии, наиболее выгодные для себя и наименее выгодные для противника.

Однако в экономической практике во многих задачах принятия решений существенно важным элементом является неопределенность другого вида. Эта неопределенность не связана с сознательным целенаправленным противодействием противника и заключается в том, что лицо, принимающее решение недостаточно информировано об объективных внешних условиях, в которых будет приниматься решение. Неопределенность такого вида может порождаться различными причинами: нестабильностью экономической ситуации, рыночной конъюнктурой, курсами валют, уровнем инфляции, налоговой политикой, изменяющимся покупательским спросом и т.д.

То есть, во всех задачах подобного рода выбор решения зависит от состояний объективной (экономической) действительности, называемой в модели «природой», а математические модели подобных конфликтных ситуаций называются «игрой с природой».

Таким образом, в игре с природой осознанно действует только один игрок, а именно, лицо, принимающее решение. «Природа» является вторым игроком, но не противником первого игрока, так как она осознанно против первого игрока не действует, принимая то или иное свое состояние неопределенным образом, конкретных целей в игре не преследует и безразлично к результату игры. Поэтому термин «природа» характеризует некую объективную реальность, которую не следует понимать буквально, хотя иногда это характеризует и действительные состояния природы.

Изучение игр с природой должно также начинаться с построения платежной матрицы, что является наиболее трудоемким и ответственным этапом при принятии решений, так как ошибки в платежной матрице не могут быть компенсированы никакими вычислительными методами.

Пусть игрок имеет возможных стратегий 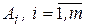, а природа 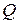может находиться в одном из возможных состояний , которые можно рассматривать как ее «стратегии». Тогда матрицу игры с природой можно представить в виде, аналогичном платежной матрице матричной игры, как 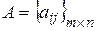, или

, (4.1)

где 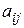- выигрыш игрока при выборе им стратегии и при состоянии природы . Матрица игры с природой содержательно отличается от платежной матрицы антагонистической матричной игры тем, что элементы столбцов матрицы (4.1) не являются проигрышами природы при соответствующих ее состояниях, то есть выигрыши 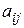платит не природа, а некая «третья сторона», или совокупность сторон, влияющих на принятие решений игроком.

С одной стороны задача выбора игроком чистой или смешанной стратегии в игре с природой проще, чем в матричной игре, так как в этом случае со стороны природы отсутствует систематическое противодействие игроку. С другой стороны, эта задача осложняется наличием неопределенности, связанной с дефицитом осведомленности игрока о характере проявления состояний природы.

В игре с природой также можно доминировать (мажорировать) стратегии, что может позволить уменьшить размерность платежной матрицы. Например, в игре с матрицей размерности :

стратегия доминирует стратегии и , поэтому их можно «удалить». Тогда размерность матрицы игры будет равна :

,

число строк в которой на 2 меньше, чем в исходной матрице. Таким образом, и в играх с природой можно и нужно пользоваться принципом доминирования стратегий игрока (строк матрицы игры). Однако этот принцип недопустим для второго игрока-природы, поскольку природа не стремится к выигрышу в игре, а действует неосознанно. Так, например, в последней матрице пятый столбец доминирует первый, второй и третий столбцы ( , и ). Поэтому в матричной игре эти столбцы можно было бы удалить. Но в игре с природой этого делать нельзя. Это обстоятельство является еще одним свойством, отличающим игры с природой от матричных игр.

При решении вопроса о выборе возможной стратегии в игре с природой игрок должен исходит из матрицы выигрышей. Однако она не всегда адекватно отражает имеющуюся ситуацию. На выбор стратегии должны влиять не только выигрыши, составляющие матрицу игры, но и показатели «удачности» и «неудачности» выбора данной стратегии при данном состоянии природы, и благоприятности этого состояния для увеличения выигрыша.

Показателем благоприятности состояния природы 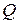называется наибольший выигрыш при этом состоянии, то есть наибольший элемент - го столбца:

. (4.2.)

И для характеристики степени удачности применения игроком стратегии 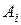при состоянии природы вводят понятие «риска».

Риском 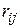игрока при выборе им стратегии при состоянии природы называется разность между показателем благоприятности и выигрышем :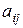

, (4.3)

То есть риск – это разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием среды будет , и выигрышем, который он получит, не имея этой информации.

Таким образом, риск 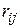игрока представляет собой упущенную возможность максимального выигрыша при данном состоянии природы. Эта упущенная возможность определяется (см. (3)) невыигранной частью максимального выигрыша. Следовательно, величину риска можно интерпретировать как своеобразную плату за отсутствие информации о действительном состоянии природы. Другими словами, точная информация о действительном состоянии природы позволяет игроку выбрать ту стратегию , при которой его выигрыш будет максимальным ( ).

Если ввести величину:

, (4.4)

представляющую собой наименьший выигрыш игрока при состоянии природы , то можно установить границу изменения рисков, как:

, (4.5.)

где разность называют колебанием выигрышей при состояниях природы .

Для данной матрицы выигрышей матрица рисков имеет ту же размерность и следующий вид:

. (4.6)

Отметим, что матрица выигрышей (4.1) однозначно определяет матрицу рисков (4.6), так как каждый элемент 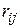этой матрицы однозначно определяется по формулам (4.3). Обратное не верно, то есть одна и та же матрица рисков может соответствовать разным матрицам выигрышей.

№ 4.1.Построить матрицу рисков для матрицы выигрышей

(4.7)

Решение. Вычислим показатели благоприятности по формулам (4.2):

, , , .

Тогда матрица рисков будет иметь вид:

. (4.8)

Матрица рисков проясняет некоторые нюансы рассматриваемой игры с природой. Например, если игрок выбирает стратегию , то при состояниях природы и он получает одинаковые выигрыши . Однако эти выигрыши не являются равноценными в смысле рисков, так как удачность выбора стратегии по отношению к состояниям природы и разная. Благоприятность состояния природы для возможности увеличения выигрыша равна , а для равна . поэтому риски игрока при выборе стратегии и при состояниях природы и соответственно равны: . Другими словами, при состоянии природы игрок мог бы выиграть по максимуму величину , а выиграл, придерживаясь стратегии , 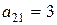ед., «проиграв» всего ед. А при состоянии природы проиграл 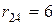ед. Таким образом, выбор стратегии по отношению к состоянию - более удачлив, чем по отношению к состоянию природы . Именно эту ситуацию и отражает матрица рисков (4.8).

В этом примере мы сравнили одинаковые выигрыши при одной и той же стратегии игрока, но при разных состояниях природы. При этом было показано, что эти результаты могут быть неравноценными в смысле рисков. Одинаковые же выигрыши при разных стратегиях, но при одном и том же состоянии природы всегда равноценны. Например, в матрице выигрышей (4.7) одинаковые выигрыши при стратегиях и , и при состоянии природы - равноценны, поскольку равны соответствующие риски .

Для решения игры с природой требуется выбрать такую чистую (или смешанную) стратегию, которая была бы наиболее выгодной по сравнению с другими. Отметим, что смешанной стратегии у игрока может и не быть, если действия игрока являются альтернативными, то есть выбор одной стратегии отвергает все другие стратегии, например при выборе альтернативных проектов.

Методы принятия решений в игре с природой зависят от того - известны или нет вероятности состояний природы. Если эти вероятности неизвестны, то имеет место ситуация полной неопределенности и это называется принятием решений в условиях полной неопределенности, а если эти вероятности известны априорно, то имеем дело с принятием решений в условиях риска.

.