
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПРИНЯТИЕ РЕШЕНИЙ В УСЛОВИЯХ РИСКА
Предположим теперь, что игроку из прошлого опыта известны не только возможные состояния природы  ,
,  , в которых может находиться природа
, в которых может находиться природа 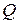 , но и соответствующие вероятности
, но и соответствующие вероятности  , с которыми природа реализует эти состояния
, с которыми природа реализует эти состояния  . В этом случае мы отступаем от условий полной неопределенности, и будем находиться в ситуации принятия решений в условиях риска.
. В этом случае мы отступаем от условий полной неопределенности, и будем находиться в ситуации принятия решений в условиях риска.
Рассмотрим некоторые критерии принятия решений в игре с природой в условиях риска.
Критерий Байеса относительно выигрышей.
По этому критерию показателем эффективности стратегии 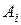 ,
,  , называется среднее значение (математическое ожидание) выигрыша с учетом вероятностей всех возможных стратегий природы:
, называется среднее значение (математическое ожидание) выигрыша с учетом вероятностей всех возможных стратегий природы:
 , (4.20)
, (4.20)
то есть  представляет собой взвешенное средне выигрышей
представляет собой взвешенное средне выигрышей  - ой строки матрицы выигрышей, взятых с весами
- ой строки матрицы выигрышей, взятых с весами  .
.
Оптимальной среди чистых стратегий по критерию Байеса будет стратегия  с максимальным показателем эффективности (4.20), то есть с максимальным выигрышем:
с максимальным показателем эффективности (4.20), то есть с максимальным выигрышем:
 (4.21)
(4.21)
То есть, выбранное таким образом решение является оптимальным не в каждом отдельном случае, а «в среднем».
№ 4.4.На промышленном предприятии готовятся к переходу на выпуск новых видов продукции  . Результаты принятых решений существенно зависят от степени обеспеченности производства материальными ресурсами
. Результаты принятых решений существенно зависят от степени обеспеченности производства материальными ресурсами  . Каждому сочетанию решений
. Каждому сочетанию решений 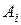 ,
,  и состояний среды
и состояний среды  соответствует определенный выигрыш - эффективность выпуска новых видов продукции. Всевозможные выигрыши представлены в платежной матрице:
соответствует определенный выигрыш - эффективность выпуска новых видов продукции. Всевозможные выигрыши представлены в платежной матрице:
 . (4.22).
. (4.22).
Предположив, что известны вероятности состояний природы  , найти оптимальную стратегию по критерию Байеса относительно выигрышей.
, найти оптимальную стратегию по критерию Байеса относительно выигрышей.
Решение. Вычислим средние выигрыши:
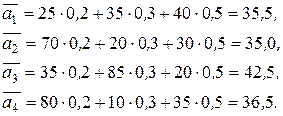
Тогда оптимальной по критерию Байеса является стратегия  , так как
, так как
 .
.
Критерий Байеса относительно рисков.
Показателем эффективности стратегии 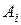 по критерию Байеса относительно рисков называется математическое ожидание рисков
по критерию Байеса относительно рисков называется математическое ожидание рисков  - ой строки матрицы
- ой строки матрицы  :
:
 (4.23)
(4.23)
И оптимальной будет стратегия с наименьшим значением среднего риска  :
:
 (4.24)
(4.24)
При этом справедливо утверждение о том, что критерии (4.21) и (4.24) эквивалентны, то есть по обоим критериям оптимальной будет одна та же стратегия.
Критерий Лапласа относительно выигрышей.
В предыдущих двух критериях Байеса известные вероятности состояний природы могли быть получены, например, на основании статистических исследований. Однако часто складывается такая ситуация, при которой мы лишены возможности определить эти вероятности. Но, желая принять решение в условиях риска, мы вынуждены оценивать эти вероятности состояний природы субъективно. Существуют различные методы численной субъективной оценки степени правдоподобности состояний природы. Один из таких способов заключается в том, что мы считаем их равновероятными:  То есть мы не можем отдать предпочтение ни одному из состояний природы. Этот принцип называют еще принципом «недостаточного основания» Лапласа.
То есть мы не можем отдать предпочтение ни одному из состояний природы. Этот принцип называют еще принципом «недостаточного основания» Лапласа.
Таким образом, показатель эффективности будет равен:
 ,
,
а наилучшая стратегия определяется по формуле (4.21).
№ 4.5. Найдите оптимальную стратегию в условиях № 4.4 по критерию Лапласа.
Решение. Вычислим средние выигрыши:

Следовательно, оптимальной по критерию Лапласа является стратегия  , так как:
, так как:
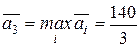 .
.
Аналогично рассматривается критерий Лапласа и относительно рисков.
Критерий Байеса относительных значений вероятностей состояний природы с учетом выигрышей.
Предположим, что вероятности состояний природы нам неизвестны, но мы имеем представление о том, какие состояния природы более правдоподобны, какие - менее правдоподобны. Это позволит представить (проранжировать) неизвестные вероятности состояний природы в виде убывающей или возрастающей числовой последовательности.
Например, можно считать, что последовательность неизвестных вероятностей  состояний природы пропорциональна членам некоторой монотонной последовательности положительных чисел
состояний природы пропорциональна членам некоторой монотонной последовательности положительных чисел  :
:
 . (4.25)
. (4.25)
Учитывая, что  , можем получить следующие оценки вероятностей:
, можем получить следующие оценки вероятностей:
 . (4.26).
. (4.26).
№ 4.6. Найдите оптимальную стратегию в условиях № 4.4, если есть основания считать, что вероятности состояний природы образуют строго убывающую числовую последовательность, пропорциональную убывающей арифметической прогрессии 3, 2, 1, то есть:
 .
.
Решение. Вычислим оценки вероятностей состояний природы по формуле (4.26):
 .
.
Тогда средние выигрыши будут равны:
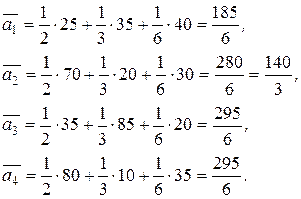
Следовательно, игроку можно порекомендовать сделать выбор между стратегиями  и
и  с наибольшими средними выигрышами.
с наибольшими средними выигрышами.
Аналогичный критерий можно рассмотреть и для матрицы рисков.
Заметим также, что когда речь идет о среднем выигрыше, то речь идет о возможности многократного повторения игры (акта принятия решений). И условность рассмотренных выше критериев состоит в том, что требуемого количества повторений чаще всего может и не быть.
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТА В ИГРАХ С ПРИРОДОЙ
Рассмотрим теперь вопрос о том, в каких случаях следует проводить эксперименты с целью получения дополнительной статистической информации о состояниях природы для принятия более эффективных решений в условиях риска.
Рассмотрим сначала так называемый «идеальный» эксперимент, в результате проведения которого игрок получает точное значение того состояния природы, которое имеет место в данной ситуации. В качестве критерия принятия решений рассмотрим критерий Байеса.
Без проведения эксперимента в качестве оптимальной стратегии по критерию Байеса относительно выигрышей выбиралась стратегия  с максимальным показателем эффективности (4.21):
с максимальным показателем эффективности (4.21):
 . (4.27)
. (4.27)
Если в результате проведенного эксперимента выяснилось, например, что природа будет находиться в состоянии  , то в качестве оптимальной надо выбирать стратегию, при которой достигается наибольший выигрыш:
, то в качестве оптимальной надо выбирать стратегию, при которой достигается наибольший выигрыш:
 ,
,
где  ,
,  -показатель благоприятности состояния природы
-показатель благоприятности состояния природы  . То есть надо выбирать такую стратегию, чтобы наибольший элемент
. То есть надо выбирать такую стратегию, чтобы наибольший элемент 
 -столбца матрицы
-столбца матрицы  находился в строке, соответствующий этой стратегии. Однако такое решение мы можем принять только после проведения эксперимента. А нам нужно решить заранее вопрос о целесообразности проведения эксперимента, про который известно только, что он является идеальным, и не известно, в каком именно состоянии
находился в строке, соответствующий этой стратегии. Однако такое решение мы можем принять только после проведения эксперимента. А нам нужно решить заранее вопрос о целесообразности проведения эксперимента, про который известно только, что он является идеальным, и не известно, в каком именно состоянии  будет находиться природа
будет находиться природа 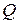 , а следовательно, нам не известен размер выигрыша игрока
, а следовательно, нам не известен размер выигрыша игрока  . Следовательно, разумно рассмотреть взвешенное среднее выигрышей
. Следовательно, разумно рассмотреть взвешенное среднее выигрышей  с весовыми коэффициентами
с весовыми коэффициентами  , то есть выигрыш в случае идеального эксперимента можно определить как:
, то есть выигрыш в случае идеального эксперимента можно определить как:
 . (4.28)
. (4.28)
Тогда средний выигрыш игрока  с применением идеального эксперимента вырастет на величину
с применением идеального эксперимента вырастет на величину  . Таким образом, проведение эксперимента имеет смысл, если стоимость
. Таким образом, проведение эксперимента имеет смысл, если стоимость  такого эксперимента удовлетворяет условию:
такого эксперимента удовлетворяет условию:
 . (4.29)
. (4.29)
№ 4.7.Определить стоимость идеального эксперимента в условиях № 4.4.
Решение. Вычислим показатели благоприятности состояний природы:

Тогда

Следовательно, так как  , то стоимость эксперимента
, то стоимость эксперимента  будет меньше, чем
будет меньше, чем
 ед.
ед.
То есть если стоимость эксперимента 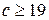 ед., то эксперимент проводить невыгодно.
ед., то эксперимент проводить невыгодно.
Можно решить эту задачу и в терминах рисков, а именно:
 . (4.30).
. (4.30).
При этом получаются те же самые результаты, что и по условию (4.29).
Теперь рассмотрим вопрос о проведении эксперимента, не являющегося идеальным, то есть позволяющего лишь уточнить вероятности состояний природы. В общем случае можно предположить, что такой эксперимент  приводит к появлению одного из несовместных событий
приводит к появлению одного из несовместных событий 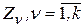 (исходов эксперимента), вероятности которых зависят от того состояния природы
(исходов эксперимента), вероятности которых зависят от того состояния природы  , при котором он проводился.
, при котором он проводился.
Предположим, что эти условные вероятности  событий
событий  , при условии, что природа находится в состоянии
, при условии, что природа находится в состоянии  , известны. Тогда по формулам Байеса можно пересчитать вероятности состояний природы, как
, известны. Тогда по формулам Байеса можно пересчитать вероятности состояний природы, как
 , (4.31)
, (4.31)
или
 ,
,
где  - априорные вероятности состояний природы;
- априорные вероятности состояний природы;  - апостериорные вероятности состояний природы, при условии, что результатом эксперимента будет
- апостериорные вероятности состояний природы, при условии, что результатом эксперимента будет  ;
;  - вероятности исхода
- вероятности исхода 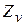 эксперимента, вычисляемые по формуле полной вероятности:
эксперимента, вычисляемые по формуле полной вероятности:
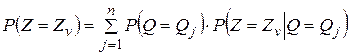 . (4.32)
. (4.32)
Пусть
 ,
,  ,
,  -
-
показатель эффективности стратегии  по критерию Байеса с апостериорными вероятностями состояний природы
по критерию Байеса с апостериорными вероятностями состояний природы  ;
;
 -
-
максимальный средний выигрыш при исходе эксперимента  ;
;
 -
-
взвешенно среднее максимальных выигрышей  с весовыми коэффициентами, равными полным вероятностям
с весовыми коэффициентами, равными полным вероятностям  событий
событий  , вычисляемым по формулам (4.32).
, вычисляемым по формулам (4.32).
Тогда средний выигрыш игрока  с применением неидеального эксперимента вырастет на величину
с применением неидеального эксперимента вырастет на величину  . Таким образом, проведение эксперимента имеет смысл, если стоимость такого эксперимента
. Таким образом, проведение эксперимента имеет смысл, если стоимость такого эксперимента  удовлетворяет условию, аналогичному (4.29):
удовлетворяет условию, аналогичному (4.29):
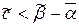 . (4.33)
. (4.33)
Можно решить эту задачу и в терминах рисков. При этом результат (4.33) не изменится.
4.8.Определить стоимость проведения эксперимента в условиях № 4.4, если матрица условных вероятностей исходов эксперимента имеет вид:

| 
| 
| 
|

| 0,6 | 0,25 | 0,15 |

| 0,3 | 0,55 | 0,15 |

| 0,1 | 0,25 | 0,65 |
Решение. Вычисление апостериорных вероятностей состояний природы представим в виде расчетной таблицы:
Таблица 4.1

|

| 
| 
| 
| ||||||

| 
| 
| 
| 
| 
| 
| 
| 
| ||

| 0,2 | 0,6 | 0,25 | 0,15 | 0,12 | 0,05 | 0,03 | 0,462 | 0,147 | 0,075 |

| 0,3 | 0,3 | 0,55 | 0,15 | 0,09 | 0,165 | 0,045 | 0,346 | 0,485 | 0,113 |

| 0,5 | 0,1 | 0,25 | 0,65 | 0,05 | 0,125 | 0,325 | 0,192 | 0,368 | 0,812 |

| 0,26 | 0,34 | 0,40 |
Пусть исходом эксперимента будет  , с апостериорными вероятностями состояний природы 0,462, 0,346 и 0,192 соответственно. Вычислим показатели эффективности стратегий игрока:
, с апостериорными вероятностями состояний природы 0,462, 0,346 и 0,192 соответственно. Вычислим показатели эффективности стратегий игрока:
 ,
,
 ,
,
 ,
,
 ,
,
Тогда максимальный средний выигрыш при исходе эксперимента  будет равен:
будет равен:
 ед.
ед.
Пусть исходом эксперимента будет  , с апостериорными вероятностями состояний природы 0,147, 0,485 и 0,368 соответственно. Вычислим показатели эффективности стратегий игрока:
, с апостериорными вероятностями состояний природы 0,147, 0,485 и 0,368 соответственно. Вычислим показатели эффективности стратегий игрока:
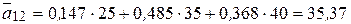 ,
,
 ,
,
 ,
,
 ,
,
Тогда максимальный средний выигрыш при исходе эксперимента  будет равен:
будет равен:
 ед.
ед.
Пусть исходом эксперимента будет  , с апостериорными вероятностями состояний природы 0,075, 0,113 и 0,812 соответственно. Вычислим показатели эффективности стратегий игрока:
, с апостериорными вероятностями состояний природы 0,075, 0,113 и 0,812 соответственно. Вычислим показатели эффективности стратегий игрока:
 ,
,
 ,
,
 ,
,
 ,
,
Тогда максимальный средний выигрыш при исходе эксперимента  будет равен:
будет равен:
 ед.
ед.
Вычислим взвешенно среднее максимальных выигрышей  с весовыми коэффициентами, равными полным вероятностям
с весовыми коэффициентами, равными полным вероятностям  событий
событий  :
:
 ед.
ед.
Следовательно, так как  , то стоимость эксперимента
, то стоимость эксперимента  будет меньше, чем
будет меньше, чем
 ед.
ед.
То есть если стоимость эксперимента  ед., то эксперимент проводить невыгодно.
ед., то эксперимент проводить невыгодно.
Выше мы рассмотрели вопрос о том – выгодно, или невыгодно проводить единичный эксперимент. Аналогичным образом можно заранее выяснить, выгодно ли провести эксперимент несколько раз.
Дата добавления: 2015-01-29; просмотров: 1230; Мы поможем в написании вашей работы!; Нарушение авторских прав |