НЕОПРЕДЕЛЕННОСТИ

Рассмотрим игру с природой, в которой вероятности состояния природы неизвестны, и отсутствует всякая возможность получения о них какой-либо статистической информации. То есть мы находимся в состоянии полной неопределенности, связанной с отсутствием информации о вероятностях состояний среды (природы).

В таких моделях для определения наилучших решений используются, например, следующие критерии: максимикса, Вальда, Сэвиджа и Гурвица.

Критерий максимакса. Это критерий крайнего оптимизма, миксимизирующая максимальные выигрыши для каждого состояния природы по формуле

. (4.9)

Для матрицы (4.7) этот критерий дает , что соответствует стратегии .

Таким образом, максимаксный критерий является критерием крайнего оптимизма, так как он ориентирует лицо, принимающее решение, на наилучшее для него состояние природы и, как следствие отсюда, - порой легкомысленное «шапкозакидательское» поведение при выборе стратегии. Вместе с тем, ситуации, требующие применения этого критерия, в экономике не так уж редки. Этим критерием пользуются не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение и вынужденные руководствоваться принципом «пан или пропал».

Максиминный критерий Вальда. При применении данного критерия природа рассматривается как агрессивно настроенный и сознательно действующий противник, как в матричной игре. Поэтому выбирается стратегия, гарантирующая выигрыш не меньший чем «нижняя цена игры с природой»:

. (4.10)

Для матрицы (4.7) этот критерий дает

.

что соответствует стратегии .

В соответствии с этим критерием, из всех самых неудачных результатов выбирается самый лучший. Это перестраховочная позиция крайнего пессимизма, рассчитанная на худший случай. Такая стратегия приемлема, например, когда игрок не столько хочет выиграть, сколько не хочет проиграть. Принципом критерия Вальда часто пользуются в обиходе, что подтверждается такими поговорками, как «береженого бог бережет» и т.д.

Выбранное таким образом решение полностью исключает риск. Это означает, что принимающий решение не может столкнуться с более худшим результатом, чем тот, на который он ориентируется. Это свойство заставляет считать критерий Вальда одним из фундаментальных. Поэтому в технических и экономических задачах он применяется чаще всего как сознательно, так и неосознанно. Однако в практических ситуациях излишний пессимизм этого критерия может оказаться очень невыгодным.

Применение этого критерия может быть оправдано, если ситуация, в которой принимается решение, характеризуется следующими обстоятельствами:

Ÿ о вероятности появления того или иного состояния ничего не известно;

Ÿ с появлением того или иного состояния необходимо считаться;

Ÿ реализуется лишь малое количество решений;

Ÿ не допускается никакой риск.

Критерий минимального риска Сэвиджа. Этот критерий аналогичен критерию Вальда, только игрок в этой ситуации руководствуется матрицей рисков (4.6) и выбирает стратегию, при которой достигается минимально возможный из крупных рисков:

, (4.11)

Для матрицы (4.8) получаем

.

То есть, лучшей стратегией по этому критерию является стратегия .

Хотя критерии Сэвиджа и Вальда являются критериями крайнего пессимизма, но в общем случае они не эквивалентны, то есть могут выбирать разные оптимальные стратегии, в чем мы убедились на приведенных выше примерах.

Обобщенный критерий пессимизма-оптимизма Гурвица относительно выигрышей с коэффициентами .

Переставим выигрыши при каждой стратегии 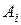(т.е. элементы каждой строки матрицы (4.1)), расположив их в неубывающем порядке. Обозначим элементы полученной матрицы через , а саму матрицу как :

, (4.12)

где

. (4.13)

Например, матрица (4.7) примет вид:

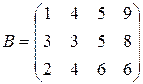(4.12')

В силу неравенств (4.13) в первом столбце матрицы расположены минимальные выигрыши 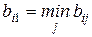, а в последнем – максимальные . Для некоторых номеров и возможны и равенства .

Введем неотрицательные числа , удовлетворяющие условию:

.

Тогда показателем эффективности стратегии 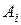по данному критерию будет число:

, (4.14)

а оптимальной стратегией будет та, при которой достигается максимум (4.14):

, (4.15)

Числа

и ,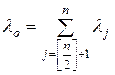

называются соответственно показателями пессимизма и оптимизма. Здесь - целая часть числа . Тогда коэффициенты , , можно выбирать следующим образом: чем ситуация опаснее, тем больше возникает желание подстраховаться, и тем ближе к единице должен быть коэффициент пессимизма . В более безопасной ситуации ближе к единице должен быть коэффициент оптимизма .

Таким образом, в данном критерии коэффициенты и выражают количественную меру соответственно пессимизма и оптимизма игрока , выбирающего коэффициенты .

Если , а , то критерий – более «оптимистичный» чем «пессимистичный». Если , а - более «пессимистичный», чем «оптимистичный». А если - то «реалистичный».

Рассмотрим теперь вопрос о формализации метода выбора коэффициентов в обобщенном критерии Гурвица относительно выигрышей.

Пусть

-

- сумма выигрышей по столбцам матрицы ;

-

- среднее значение выигрышей , расположенных в - ом столбце;

-

- сумма всех возможных выигрышей игрока .

С учетом свойств матрицы получаем условие:

или

.

Поэтому, в случае выбора игроком более пессимистичной стратегии можно предложить выбрать коэффициенты пропорциональными средним выигрышам:

,

что приводит к следующим формулам для вычисления :

, . (4.16)

Если же игрок преисполнен оптимизма и считает ситуацию достаточно безопасной, то можно предложить выбрать коэффициенты следующим образом:

,

или, как:

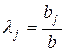, . (4.17)

В случае реалистичного подхода можно предложить .

Отметим, что для применения формул (4.16) и (4.17) необходимо, чтобы все должны быть или положительными, или отрицательными.

№ 4.2.Найти оптимальную стратегию в игре с природой (4.7) по обобщенному критерию Гурвица.

Решение. Вычислим:

и .

Тогда, если игрок придерживается пессимистической стратегии, то

,

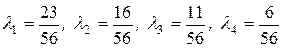и .

Вычислим показатели эффективности стратегий по формулам (4.14):

,

,

.

Следовательно, оптимальной в этом случае является стратегия , так как

.

Если игрок придерживается более оптимистичной стратегии, то

,

и .

Тогда показатели эффективности будут равны:

,

,

.

и оптимальной будет стратегия , так как:

.

Если игрок придерживается реалистичной стратегии, то:

,

,

,

и игрок может выбирать между стратегиями и .

Отметим, что аналогичным образом можно рассмотреть и применение обобщенного критерия Гурвица применительно к матрице рисков .

Частным случаем обобщенного критерия является критерий пессимизма-оптимизма Гурвица относительно выигрышей с показателем пессимизма 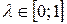. То есть:

.

Показателем эффективности стратегии 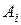по этому критерию является величина:

, (4.18)

а оптимальная стратегия определяется из условия:

. (4.19)

Этот критерий учитывает как пессимистический, так и оптимистический подходы к решению игры. А именно, при получаем критерий крайнего оптимизма, и решение совпадает с критерием максимакса; при 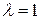получаем критерий крайнего пессимизма и решение совпадает с критерием Вальда. - характеризует склонность игрока к риску, а именно, чем ближе к 1, тем игрок менее склонен к риску.

№ 4.3.Решите № 4.2. по критерию (4.19).

Решение. Предположим, что . Тогда:

,

,

.

И в силу (4.19) оптимальной будет стратегия .

Критерий Гурвица предъявляет к ситуации, в которой принимается решение, следующие требования:

Ÿ о вероятности появления того или иного состояния природы ничего не известно

Ÿ с появлением того или иного состояния необходимо считаться;

Ÿ реализуется лишь малое количество решений;

Ÿ допускается некоторый риск.

Если по принятому критерию рекомендуется использование нескольких стратегий, то выбор между ними может производиться по дополнительному критерию, например, можно сравнивать между собой средние квадратические отклонения выигрышей.

Предположим, что один из рассмотренных выше критериев, рекомендует игроку выбрать стратегии или , как в № 4.2 при . Тогда вычислив средние квадратические отклонения:

,

.

можно рекомендовать из двух стратегий выбрать стратегию с меньшим значением среднего квадратического отклонения.

Общие рекомендации по выбору того или иного критерия дать затруднительно. Однако отметим следующее: если в отдельных ситуациях не допустим даже минимальный риск, то следует применять критерий Вальда; если определенный риск вполне приемлем, то можно воспользоваться критерием Сэвиджа. Можно рекомендовать одновременно применять поочередно различные критерии. После этого среди нескольких вариантов, отобранных таким образом, в качестве оптимального приходится волевым решением выделять некоторое окончательное решение.

Такой подход позволяет, во-первых, лучше проникнуть во все внутренние связи проблемы принятия решений и, во-вторых, ослабляет влияние субъективного фактора. Кроме того, различные критерии часто приводят к одному результату.

Таким образом, в случае отсутствия информации о вероятностях состояния среды теория не дает однозначных и математически строгих рекомендаций по выбору критериев принятия решений. Это объясняется, в большей мере, не слабостью теории, а неопределенностью самой ситуации. Единственный разумный выход в подобных случаях – попытаться получить дополнительную информацию, например, путем проведения исследований или экспериментов. В отсутствие дополнительной информации принимаемые решения теоретически недостаточно обоснованы и в значительной мере субъективны. Хотя применение математических методов в играх с природой не дает абсолютно достоверного результата и последний в определенной степени является субъективным (вследствие произвольности выбора критерия), оно, тем не менее, создает некоторое упорядочение, имеющихся в распоряжении игрока данных, и способствует повышению качества принимаемых решений, а именно:

1) Задается множество состояний природы.

2) Выигрыши и проигрыши при различных сочетаниях состояний .

Такое упорядочение представлений о проблеме само по себе способствует повышению качества принимаемых решений.