Распределение энергии по степеням свободы.

Средняя энергия (из вывода основного уравнения кинетической теории газов), приходящаяся на одну молекулу ` 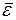. Если считать молекулу шариком (как в одноатомном газе), то средняя энергия такой частицы определяется средней кинетической энергией ее поступательного движения. Энергию эту можно представить как сумму трех слагаемых – кинетических энергий движения молекулы по трем взаимно перпендикулярным направлениям:

,

где u_x, u, u_z – составляющие скорости молекул по трем осям координат. Из-за хаотичности молекулярного движения можно считать, что средние значения кинетических энергий по трем направлениям равны друг другу:

.

(6.8.1)

Так как согласно основному уравнению кинетической теории

,

то каждое из трех слагаемых равенства (6.8.1) равно kT/2. Разделение кинетической энергии частицы на три независимые составляющие связано с тем, что частица рассматривается как свободная материальная точка, обладающая тремя степенями свободы.

Число степеней свободы - наименьшее число линейно независимых координат, которые полностью определяют положение тела в пространстве. Значит, на каждую степень свободы одноатомной молекулы приходится энергия, равная kT/2. В классической статистической физике доказывается теорема, названная теоремой Больцмана: в совокупности большого числа молекул, находящемся в тепловом равновесии при температуре Т средняя кинетическая энергия равномерно распределена между всеми степенями свободы и для каждой степени свободы молекулы она равна kT/2.

Эта теорема называется законом равномерного распределения кинетической энергии по степеням свободы, или, законом равнораспределения.

Двух- и многоатомные газы отличаются от одноатомных числом степеней свободы. Рассмотрим двухатомную молекулу. Ее можно представить себе в виде системы, состоящей из двух атомов, расположенных на некотором расстоянии друг от друга. Будем считать, что это жесткая молекула, то есть расстояние между атомами не меняется.

Вообще говоря, такая система имеет шесть степеней свободы: три степени свободы приходится на поступательное движение центра масс, и три – возможные вращательные движения вокруг осей Ох, 0у и 0z. Однако, вращение молекулы вокруг оси 0х не вносит изменения в кинетическую энергию: E_к , где J – момент инерции системы, J ~ mr². Величины угловой скорости w вокруг оси 0х, которые могут быть достигнуты, практически таковы, что значительно меньше кинетической энергии поступательного движения. Вращение относительно оси 0х неэффективно. Поэтому для описания возможных вращений достаточно двух координат. Следовательно, число степеней свободы жесткой двухатомной молекулы равно 5, из них три поступательные и две вращательные степени свободы. Но атомы в молекуле не всегда жестко связаны друг с другом.

Трехатомный газ имеет 6 степеней свободы. Если молекула состоит из n атомов, не жестко связанных, то она имеет 3n степеней свободы (каждый атом имеет три степени свободы). Из этого числа три степени свободы поступательные и три вращательные, за исключением случая, когда атомы расположены на одной прямой, – тогда вращательных степени свободы только две. Остальные 3n-6 степени свободы являются колебательными.

Итак, если молекула обладает i степенями свободы, то средняя энергия молекулы

.

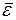(6.8.2)