ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ

Основные понятия.

1.1. ОСНОВНЫЕ ГИПОТЕЗЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ!

При построении теории расчета невозможно отразить все многообразие свойств реальных материалов, поэтому приходится делать целый ряд допущений, упрощающих расчеты.
1. В курсе сопротивления материалов рассматривается идеализированное тело, которое считается сплошным (без пустот) и однородным.
Это означает, что свойства материала не зависят от формы и размера тела и одинаковы во всех его точках.
2. Упругие свойства материала во всех направлениях одинаковы, т.е. материал тела обладает упругой изотропией.
3. Тело считается абсолютно упругим, если после устранения причин, вызывающих деформацию, оно полностью восстанавливает свои первоначальные форму и размеры.
Это допущение справедливо лишь при напряжениях, не превышающих предел упругости.
4. Деформации материала конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке (закон Гука).
Закон Гука справедлив лишь при напряжениях, не превышающих предел пропорциональности.
5. Деформации элементов конструкции в большинстве случаев настолько малы, что можно не учитывать их влияние на взаимное расположение нагрузок и на расстояние от нагрузок до любых точек конструкции.
6. Результат воздействия на конструкцию системы нагрузок равен сумме результатов воздействия каждой нагрузки в отдельности (принцип независимости действия сил).
Принцип независимости действия сил не распространяется на работу внешних и внутренних сил и на потенциальную энергию.
7. Поперечное сечение, плоское до деформации, остается плоским и после деформации (гипотеза плоских сечений Бернулли).

1.2. РАСЧЕТНАЯ СХЕМА

В сопромате расчеты производятся с помощью расчетных схем.
Реальный объект, освобожденный от несущественных особенностей, носит название расчетной схемы.
Реальные стержни изображаются их осями на расчетной схеме. Нагрузку, приложенную к небольшим участкам поверхности, заменяют силой, приложенной в точке, которую называют сосредоточенной и обозначают через Р.
Схематизируются и свойства материала. Принято рассматривать все материалы как однородную сплошную среду.
Вводятся упрощения и в геометрию конструкции. Так, все реальные тела, один размер у которых - длина, на много больше двух других (поперечных), сводятся к схеме бруса (рис. 1.1).

1.3. ВНУТРЕННИЕ СИЛЫ!

Между соседними частицами тела (молекулами, кристаллами, атомами) всегда имеются определенные силы взаимодействия, иначе внутренние силы.
Эти силы стремятся сохранить тело как единое целое. Внешние силы, наоборот, всегда стремятся вызвать деформацию тела.
Внутренние силы действуют и при отсутствии внешней нагрузки, но в этом случае они взаимно уравновешены и никаким образом себя не проявляют. Возможность оценить их уровень и почувствовать их наличие появляется только при приложении к телу внешних сил.
Приложение к телу внешней нагрузки вызывает изменение внутренних сил, т.е. появление дополнительных внутренних сил. В сопротивлении материалов изучают и вычисляют только те дополнительные внутренние силы, которые появляются в результате нагружения. Таким образом, возникает необходимость связать и выразить внутренние усилия через внешние.

1.4. КЛАССИФИКАЦИЯ ВНЕШНИХ СИЛ!

Внешними силами называют силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами. Если же нагрузка распределена по поверхности тела или его части, то такую нагрузку называют распределенной
В расчетной схеме нагрузку, распределенную по поверхности (рис. 1.2) приводят к плоскости, совпадающей с продольной осью, в результате чего получается нагрузка, распределенная по линии. Мерой такой нагрузки является ее интенсивность q - величина нагрузки на единицу длины. Размерность - Н/м. Равнодействующая распределенной нагрузки численно равна площади ее эпюры и приложена в центре ее тяжести.

Рис. 1.2
Кроме тoгo, встречаются нагрузки в виде сосредоточенного момента (пары сип). Есть несколько способов изображения моментов (рис. 1.3).

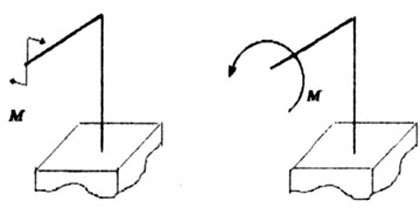
Рис. 1.3
Тогда М - это крутящий момент (рис. 1.4).

Рис. 1.4

Так изображается сипа, идущая к нам.

Так изображается сила, идущая от нас.

1.5. МЕТОД СЕЧЕНИЙ (РОЗУ)!

Так как внутренние силы взаимно уравновешены и стоит задача выразить их через внешние, то необходимо выполнить такую операцию, чтобы внутренние силы стали явными. Например для стержня можно применить прием мысленного рассечения на две части плоскостью, перпендикулярной продольной оси. Затем отбросить одну из полученных частей, что позволяет превратить внутренние силы, для целого стержня, во внешние для оставленной части стержня (рис.1.5).

Рис. 1.5
Силы взаимодействия будут в каждой точке проведенного сечения (рис. 1.6).

Рис. 1.6
Эту систему большого числа сил по правилам теоретической механики можно привести к одной точке (центру тяжести поперечного сечения), в результате чего получим главный вектор R и главный момент М (рис. 1.7).
2. Отбрасываем одну часть

Рис. 1.7
Теперь спроектируем на три оси (продольную z и две взаимно-перпендикулярные поперечные х и у). В результате получим шесть внутренних силовых факторов: три силы N, Qx Qy и три момента Мx, My и Мz
Сила N называется продольной силой, силы Qx и Qy - поперечные силы. Момент относительно оси z - Мz - крутящий момент, и моменты Мx, My относительно поперечных осей - изгибающие.
Каждому из внутренних усилий соответствует определенный вид деформации (изменение формы), бруса. Например, продопьной силе N соответствует растяжение (или сжатие) бруса.
3. Заменяем

Рис. 1.8
Таким образом, рассматривается одна из полученных при рассечении частей стержня, которая нагружена приложенными к этой части внешними силами и шестью внутренними усилиями (рис. 1.8).
4. Уравновешиваем
Для установления связи внутренних и внешних сил можно к этой части применить уравнения равновесия, (уравновешиваем), так как известно, что если тело находится в целом в равновесии, то в равновесии и любая его часть.

Рассмотрим, например, уравнение . Из внутренних усилий на ось z проектируется только продольная сила N.
Тогда
где - проекция всех внешних сил, действующих на оставленную часть стержня, на ось z.
Отсюда вытекает следующее определение: продольная сила N численно равна алгебраической сумме проекций на ось стержня всех внешних сил, расположенных по одну сторону (рассматриваемую) от проведенного сечения.
Аналогичные определения для Qx, Qy, Мx, My, и Mz. По первым буквам выполняемых операций (рассекаем, отбрасываем, заменяем и уравновешиваем) метод сечений иногда называют методом РОЗУ

1.6. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ СИЛОВЫХ ФАКТОРОВ

Задача определения наибольших напряжений начинается с поиска сечения, в котором действуют наибольшие внутренние усилия.
Наибольший изгибающий момент в случае прямого поперечного изгиба консольной балки, нагруженной сосредоточенной силой Р (рис. 1.9) будет в сечении А у заделки, так как здесь действует максимальный изгибающий момент, равный МA = Р*а.

Рис. 1.9
Опасное сечение - это поперечное сечение, в котором действуют наибольшие внутренние усилия.
Где будет располагаться опасное сечение в более сложном случае загружения (рис. 1.10) сразу ответить достаточно трудно, так как сосредоточенный изгибающий момент М и распределенная нагрузка q изгибают балку вниз, а сосредоточенная сила Р - вверх, при этом величины моментов от каждого вида нагрузки различны.

Рис. 1.10
Поэтому для сложных случаев загружения необходимо знать закон изменения по длине балки изгибающего момента или другого внутреннего усилия (например, продольной силы N, поперечной силы Q или крутящего момента Мкр).
Этот закон можно изобразить с помощью специальных графиков, называемых эпюрами.
Эпюра - это график, изображающий закон изменения внутреннего усилия по длине стержня. Каждая ордината эпюры представляет собой величину усилия в соответствующем поперечном сечении стержня.
Построение эпюр по методу сечений выполняется в четыре этапа.
Из составленных на 4-ом этапе метода сечений уравнений выражаем искомые внутренние силовые факторы: N, Qx, Qy, Мx, Мy, и Мz (Мкр.)
С использованием полученных выражений строим графики изменения ВСФ - Л/, Мх и т.д. по длине стержня - эпюры.

ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ

В случаях растяжения-сжатия (а) или кручения (б) ординаты эпюр продольных сил или крутящих моментов также показывают их величины в соответствующих поперечных сечениях (рис.1.11а.б).

Рис. 1.11
Любое внутреннее усилие определяется по внешним нагрузкам при помощи метода сечений.
Каждая эпюра на своих участках имеет знаки.
Правила знаков для внутренних усилий, применяемые в машиностроении.
1. Продольная сила N считается положительной, если она вызывает растяжение отсеченной части и отрицательной, если вызывает ее сжатие.
2. Поперечная сила О считается положительной, если она вращает отсеченную часть по ходу часовой стрелки и отрицательной, если вращение происходит против хода часовой стрелки.
3. Эпюра изгибающих моментов строится на сжатых волокнах. Изгибающий момент положителен, если сжаты верхние волокна отсеченной части, и отрицателен, если сжаты нижние волокна
4. Правило знаков для крутящего момента принимается произвольным.
Обычно уславливаются, что при взгляде на нормаль к отсеченной части внутренний крутящий момент считается положительным, если он крутит отсеченную часть по часовой стрелке.
При изгибе между поперечной силой Q, изгибающим моментом М, углом поворота поперечного сечения и прогибом Y существуют дифференциальные зависимости, позволяющие установить следующие характерные особенности эпюр
1. Записываем выражение изгибающих моментов для текущего сечения z, например, в консольной балке, находящейся под действием сосредоточенной силы (рис. 1.12)

Рис. 1.12
М = - P*z - уравнение прямой.
В соответствии с дифференциальной зависимостью Журавского:

Из этого следует, что на прямолинейном ненагруженном внешней пролетной нагрузкой участке стержня эпюра моментов М прямолинейна, а эпюра поперечных сил Q постоянна (рис. 1.12).
2. В точке приложения сосредоточенного изгибающего момента эпюра моментов М имеет скачок на величину этого момента, а эпюра поперечных сил О постоянна.В точке приложения сосредоточенного крутящего момента эпюра крутящих моментов Мкр имеет скачок на вепичину этого момента рис. 1.11 б).
3. В точке приложения сосредоточенной поперечной силы эпюра изгибающих моментов имеет излом острием навстречу силе, а эпюра поперечных сил - скачок на величину этой силы.
В точке приложения сосредоточенной продольной силы эпюра продольных сил А также имеет скачок на величину этой силы.
4. Записываем выражение изгибающих моментов для текущего сечения z в случае изгиба консольной балки, находящейся под действием распре-лйпвнной нагрузки (рис.1.13 а)

уравнение квадратной параболы.
В соответствии с дифференциальной зависимостью Журавского:

уравнение прямой.
Таким образом, на участке с распределенной нагрузкой эпюры изгибающих моментов М очерчены по квадратной параболе с выпуклостью навстречу действию распределенной нагрузки, а эпюра поперечных сил Q имеет вид трапеции или треугопьника. И очерчена прямой, наклонной линией АВ, при этом направление наклона (при обходе слева направо) совпадает с направлением q (рис. 1.13 а, б, в).

Рис. 1.13