НАПРЯЖЕНИЕ И РАСЧЕТ НА ПРОЧНОСТЬ

Расчет стержня круглого поперечного сечения на прочность.
Расчет на прочность выполняется с использованием условия прочности при кручении.
Во-первых, необходимо расчетным путем определить максимальные касательные напряжения, возникающие в опасном поперечном сечении. Этот расчет производится по формуле:

Предварительно необходимо определить максимальный крутящий момент Мкр, возникающий от действия внешней нагрузки.
Крутящий момент Мкр характеризует уровень внутренних сил, возникающих в стержне и уравновешивающих внешнюю нагрузку
Чем больше значение Мкр , тем выше уровень внутренних сил, возникающих в стержне.
Прочность стержня будет определять то поперечное сечение стержня, в котором крутящий момент Мкр имеет максимальное значение.
Размерность крутящего момента - Мкр: кГсм, кГм, Нм, кНм и т.д.
После определения максимального значения крутящего момента необходимо определить характеристику поперечного сечения, определяющую прочность круглого стержня при кручении, которая называется полярным моментом сопротивления и обозначается Wр.
Таким образом, определены максимальные касательные напряжения , которые определяют прочность стержня, но не дают ответа на вопрос, выдержит ли рассматриваемый стержень внешнюю нагрузку без разрушения или нет.
Для решения поставленной задачи еще необходимо знать допускаемые напряжения , в сравнении с которыми максимальных напряжений 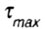и выносится решение о прочности или непрочности рассчитываемого стержня.
Определяется это с использованием условия прочности при кручении.

Таким образом, путем сравнения максимальных напряжений, возникающих в опасном сечении стержня круглого поперечного сечения 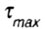c Допускаемыми и принимается решение о прочности стержня.
С использованием условия прочности возможно решение двух задач:
1. Первая задача носит название проверочной,
2. Вторая задача называется проектировочной.

Изгиб