Типы динамического поведения биологических систем

Современная практика математического моделирования показала, что наиболее содержательные и вместе с тем не слишком перегруженные деталями модели содержат, как правило, два уравнения. Именно в том случае, когда, пользуясь разделением переменных на быстрые и медленные, можно свести исходную систему к виду

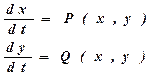
В процессе изменения состояния системы во времени переменные х, у изменяются согласно уравнениям так, что каждому состоянию соответствует пара значений (х, у). Иными словами, измеряя в последовательные моменты времени t_pt₂, ,t_n значения переменных х, у, мы представ­ляем состояние системы в виде соответствующих пар (х_;, у), (х₂, у₂), ..., (х_nу_п\ которые являются координатами точек М_р М₂, ..., М_п , изображающих движение системы.

В каждый момент времени t изображающая точка будет двигаться в соответствии с системой уравнений и каждый раз принимать положение М (х, у) в зависимости от значений x(t),y(t). Совокупность этих точек называется фазовой траекторией.

Характер фазовых траекторий отражает общие качественные черты поведения системы во времени или дает фазовый портрет системы.

Мы рассмотрим наиболее важные биологические примеры.

Модель Вольтерра «хшцник-жертва»

Эта модель отражает численности популяций жертв (х) и хищников (у), взаимодействующих друг е другом по механизму свободных соударений. Это значит, что численность жертв пропорциональна вероятности встречи их с хищниками, то есть, пропорциональна произведению ху. По такому же закону увеличивается и численность хищников в результате их встреч с жертвами. В уравнениях кинетики это соответствует бимолекулярной реак­ции (типа кху). Кроме того, происходит процесс естественной смертности хищников со скоростью, пропорциональной их количеству, то есть по ре­акции первого порядка (- ку). Жертвы размножаются со скоростью, также пропорциональной их численности в условиях, когда количество пищи для них неограниченно.

В этих упрощенных предположениях соответствующие уравнения имеют вид

- соответствующие константы скоростей или коэффициенты пропорциональности.

Исторически система Вольтерра была первой моделью, где было качественно объяснено наблюдаемое в природе периодическое изменение численности популяции видов, не зависящее от внешних воздействий. Однако этамодель слишком простая и не отражает взаимодействия видов в естественных условиях.

Для улучшения модели предлагается, например, учесть самоограничения в естественных условиях роста обеих популяций путем добавления в правые части уравнений членов второго порядка, отражающих эффект тесноты и конкуренции внутри популяции.